题目内容
17. “已知点P在直线 l 上,利用尺规作图过点P作直线 PQ⊥l”的作图方法如下:
“已知点P在直线 l 上,利用尺规作图过点P作直线 PQ⊥l”的作图方法如下:①以点P为圆心,以任意长为半径画弧,交直线l于A、B两点;
②分别以A、B两点为圆心,以大于$\frac{1}{2}$AB的长为半径画弧,两弧交于点Q;
③连接PQ.则直线 PQ⊥l.请说明此方法依据的数学原理是三线合一或到线段两端距离相等的点在线段的垂直平分线上,两点确定一条直线..
分析 根据等腰三角形的性质(三线合一)或垂直平分线的定义即可得出结论.
解答 解:三线合一或到线段两端距离相等的点在线段的垂直平分线上,两点确定一条直线.注:此题答案不唯一.
故答案为三线合一或到线段两端距离相等的点在线段的垂直平分线上,两点确定一条直线.
点评 本题考查作图-基本作图、线段垂直平分线的定义和性质等知识,解题的关键是理解题意,记住等腰三角形的性质,线段垂直平分线的定义和性质,属于基础题,中考常考题型.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
6.某保险公司一种医疗保险产品规定,住院治疗的病人享受分段报销制,报销细则如表:
张三住院治疗后得到保险公司报销金额为800元,那么他的住院医疗费为2000.
| 住院医疗费(元) | 报销率(%) |
| 不超过500元的部分 | 10 |
| 超过500元不超过1000元的部分 | 30 |
| 超过1000元不超过3000元的部分 | 60 |
| 超过3000元部分 | 90 |
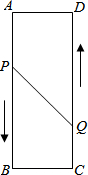 如图,矩形ABCD中,AB=16cm,AD=6cm,动点P、Q分别从A、C两点同时出发,点P以3cm/s的速度向点B移动,一直到达点B为止,点Q以2cm/s的速度向点D移动.
如图,矩形ABCD中,AB=16cm,AD=6cm,动点P、Q分别从A、C两点同时出发,点P以3cm/s的速度向点B移动,一直到达点B为止,点Q以2cm/s的速度向点D移动. 如图,在平面直角坐标系中,直线AB与y轴在正半轴、x轴正半轴分别交A、B两点,M在BA的延长线上,PA平分∠MAO,PB平分∠ABO,则∠P=45°.
如图,在平面直角坐标系中,直线AB与y轴在正半轴、x轴正半轴分别交A、B两点,M在BA的延长线上,PA平分∠MAO,PB平分∠ABO,则∠P=45°. 如图,在正方形网格中,每个小正方形的边长均相等,点A、B、O均在格点处,则cos∠AOB=$\frac{3}{5}$.
如图,在正方形网格中,每个小正方形的边长均相等,点A、B、O均在格点处,则cos∠AOB=$\frac{3}{5}$. 如图,在长方形网格中,四边形ABCD的面积为10ab.(用含字母a,b的代数式表示)
如图,在长方形网格中,四边形ABCD的面积为10ab.(用含字母a,b的代数式表示)