题目内容
5.已知A、B在数轴上分别表示a、b.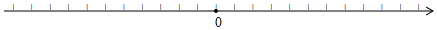
(1)对照数轴填写下表:
| a | 6 | -6 | -6 | 2 | -1.5 |
| b | 4 | 0 | -4 | -10 | -1.5 |
| A、B两点的距离 | 2 | 0 |
(3)写出数轴上到-1和1的距离之和为2的所有整数;
(4)若点C表示的数为x,代数式|x+1|+|x-2|取最小值时,相应的x的取值范围是-1≤x≤2,此时代数式|x+1|+|x-2|的最小值是3.
分析 (1)根据数轴,即可解答;
(2)根据两点间的距离,即可解答;
(3)根据数轴,即可解答;
(4)|x+1|+|x-2|的最小值,意思是x到-1的距离与到2的距离之和最小,那么x应在-1和2之间的线段上
解答 解:(1)0-(-6)=6,-4-(-6)=-4+6=2,2-(-10)=2+10=12,
故填:6,2,12;
(2)d=|a-b|;
(3)数轴上到-1和1的距离之和为2的所有整数为:-1,0,1;
(4)在数轴上|x+1|+|x-2|的几何意义是:表示有理数x的点到-1及到3的距离之和,所以当-1≤x≤2时,它的最小值为3;
故答案为:-1≤x≤2,3.
点评 本题主要考查了数轴和绝对值,掌握数轴上两点间的距离=两个数之差的绝对值,绝对值是正数的数有2个.

练习册系列答案
相关题目
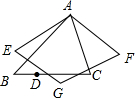 如图,△ABC中,∠BAC=60°,∠B=45°,AB=2,点D是BC上的一个动点,D点关于AB,AC的对称点分别是E和F,四边形AEGF是平行四边形,则四边形AEGF的面积的最小值是$\sqrt{3}$.
如图,△ABC中,∠BAC=60°,∠B=45°,AB=2,点D是BC上的一个动点,D点关于AB,AC的对称点分别是E和F,四边形AEGF是平行四边形,则四边形AEGF的面积的最小值是$\sqrt{3}$. 如图,在△ABC中,AB=AC=10,sinB=$\frac{3}{5}$,
如图,在△ABC中,AB=AC=10,sinB=$\frac{3}{5}$,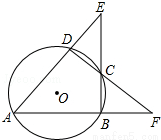 如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.
如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.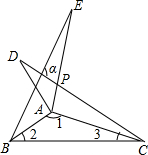 如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,若∠1:∠2:∠3=7:2:1,则∠α的度数为108°.
如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,若∠1:∠2:∠3=7:2:1,则∠α的度数为108°.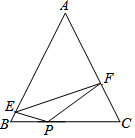 已知:如图,在△ABC中,AB=AC且tanA=$\frac{4}{3}$,P为BC上一点,且BP:PC=3:5,E、F分别为AB、AC上的点,且∠EPF=2∠B,若△EPF的面积为6,则EF=2$\sqrt{13}$.
已知:如图,在△ABC中,AB=AC且tanA=$\frac{4}{3}$,P为BC上一点,且BP:PC=3:5,E、F分别为AB、AC上的点,且∠EPF=2∠B,若△EPF的面积为6,则EF=2$\sqrt{13}$.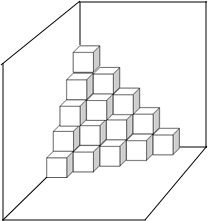 如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层…
如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层…