题目内容
6.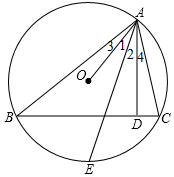 △ABC的三个顶点在⊙O上,AD⊥BC,D为垂足,E是$\widehat{BC}$的中点,求证:∠1=∠2(提示:可以延长AO交⊙O于F,连接BF).
△ABC的三个顶点在⊙O上,AD⊥BC,D为垂足,E是$\widehat{BC}$的中点,求证:∠1=∠2(提示:可以延长AO交⊙O于F,连接BF).
分析 连接OE,利用垂径定理可得OE⊥BC,再利用AD⊥BC,可得OE∥AD,然后即可证明.
解答  证明:连接OE,
证明:连接OE,
∵E是$\widehat{BC}$的中点,
∴弧BE=弧EC,
∴OE⊥BC,
∵AD⊥BC,
∴OE∥AD,
∴∠OEA=∠EAD,
∵OE=OA,
∴∠OAE=∠OEA,
∴∠1=∠2.
点评 此题主要考查学生对三角形内角和定理和圆心角、弧、弦的关系等知识点的理解和掌握,此题难度不大,关键是作好辅助线.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
18.如果|y+3|+(2x-4)2=0,那么2x-y的值为( )
| A. | 1 | B. | -1 | C. | -7 | D. | 7 |
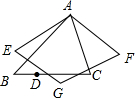 如图,△ABC中,∠BAC=60°,∠B=45°,AB=2,点D是BC上的一个动点,D点关于AB,AC的对称点分别是E和F,四边形AEGF是平行四边形,则四边形AEGF的面积的最小值是$\sqrt{3}$.
如图,△ABC中,∠BAC=60°,∠B=45°,AB=2,点D是BC上的一个动点,D点关于AB,AC的对称点分别是E和F,四边形AEGF是平行四边形,则四边形AEGF的面积的最小值是$\sqrt{3}$.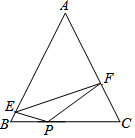 已知:如图,在△ABC中,AB=AC且tanA=$\frac{4}{3}$,P为BC上一点,且BP:PC=3:5,E、F分别为AB、AC上的点,且∠EPF=2∠B,若△EPF的面积为6,则EF=2$\sqrt{13}$.
已知:如图,在△ABC中,AB=AC且tanA=$\frac{4}{3}$,P为BC上一点,且BP:PC=3:5,E、F分别为AB、AC上的点,且∠EPF=2∠B,若△EPF的面积为6,则EF=2$\sqrt{13}$.
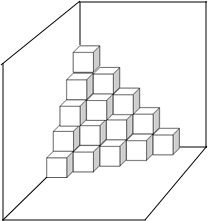 如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层…
如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层… 已知:如图,△ABC中,DE∥BC.
已知:如图,△ABC中,DE∥BC.