题目内容
9.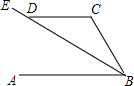 如图,已知AB∥CD,BE平分∠ABC,交CD于点D,若∠CDE=144°,则∠C=108°.
如图,已知AB∥CD,BE平分∠ABC,交CD于点D,若∠CDE=144°,则∠C=108°.
分析 根据平角等于180°求出∠BDC,再根据两直线平行,内错角相等可得∠ABE=∠BDC,根据角平分线的定义可得∠ABE=∠CBD,最后根据三角形的内角和定理列式计算即可得解.
解答 解:∵∠CDE=144°,
∴∠BDC=180°-∠CDE=180°-144°=36°,
∵AB∥CD,
∴∠ABE=∠BDC=36°,
∵BE平分∠ABC,
∴∠ABE=∠CBD=36°,
在△BCD中,∠C=180°-∠BDC-∠CBD=180°-36°-36°=108°.
故答案为:108.
点评 本题考查了平行线的性质,三角形的内角和定理,角平分线的定义,是基础题,熟记性质与概念是解题的关键.

练习册系列答案
相关题目
17.下列图形既是轴对称图形又是中心对称图形的是( )
| A. | 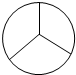 | B. | 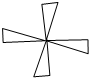 | C. | 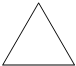 | D. |  |
4. 如图,已知AB∥CD,BC平分∠ABE,∠C=34°,则∠BED的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=34°,则∠BED的度数是( )
 如图,已知AB∥CD,BC平分∠ABE,∠C=34°,则∠BED的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=34°,则∠BED的度数是( )| A. | 17° | B. | 34° | C. | 56° | D. | 68° |
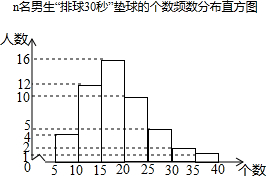 某校为了预测九年级男生“排球30秒”对墙垫球的情况,从本校九年级随机抽取了n名男生进行该项目测试,并绘制出如下的频数分布直方图,其中从左到右依次分为七个组(每组含最小值,不含最大值).根据统计图提供的信息解答下列问题:
某校为了预测九年级男生“排球30秒”对墙垫球的情况,从本校九年级随机抽取了n名男生进行该项目测试,并绘制出如下的频数分布直方图,其中从左到右依次分为七个组(每组含最小值,不含最大值).根据统计图提供的信息解答下列问题: 解不等式或不等式组.
解不等式或不等式组. 某公司现有甲、乙两种品牌的计算器,甲品牌计算器有A,B,C三种不同的型号,乙品牌计算器有D,E两种不同的型号,新华中学要从甲、乙两种品牌的计算器中各选购一种型号的计算器.
某公司现有甲、乙两种品牌的计算器,甲品牌计算器有A,B,C三种不同的型号,乙品牌计算器有D,E两种不同的型号,新华中学要从甲、乙两种品牌的计算器中各选购一种型号的计算器. 如图是4×4的正方形网格,请选取一个白色的正方形并涂上阴影,使图中阴影部分是一个中心对称图形.
如图是4×4的正方形网格,请选取一个白色的正方形并涂上阴影,使图中阴影部分是一个中心对称图形.