题目内容
14. 解不等式或不等式组.
解不等式或不等式组.(1)4x+5≥6x-3.并将解集在数轴上表示出来;
(2)$\left\{\begin{array}{l}{x-3(x-2)≤4}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$.
分析 (1)移项,合并同类项,最后把不等式的解集在数轴上表示出来即可;
(2)分别求出各不等式的解集,再求出其公共解集即可.
解答 解:(1)4x-6x≥-3-5,
-2x≥-8,
x≤4;
将解集在数轴上表示出来为:
(2)$\left\{\begin{array}{l}{x-3(x-2)≤4①}\\{\frac{1+2x}{3}>x-1②}\end{array}\right.$,
由不等式①得:x≥1,
由不等式②得:x<4.
故不等式组的解集为1≤x<4.
点评 本题考查了解一元一次不等式和在数轴上表示不等式的解集的应用,注意:解一元一次不等式得步骤是:去分母,去括号,移项,合并同类项,系数化成1.同时考查了解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
4.方程x2-4x+3=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 只有一个实数根 | ||
| C. | 没有实数根 | D. | 有两个不相等的实数根 |
6.若多项式x2-mx+9是一个完全平方式,则m的值为( )
| A. | 3 | B. | ±6 | C. | 6 | D. | ±3 |
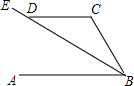 如图,已知AB∥CD,BE平分∠ABC,交CD于点D,若∠CDE=144°,则∠C=108°.
如图,已知AB∥CD,BE平分∠ABC,交CD于点D,若∠CDE=144°,则∠C=108°.