题目内容
15.为了更好治理岳阳河水质,安岳县污水处理公司计划购买10台污水处理设备,现有A、B两种型号的设备,其中每台的价格、月处理污水量如表:| A型 | B型 | |
| 价格(万元/台) | m | n |
| 处理污水量(吨/月) | 250 | 200 |
(1)求m,n的值;
(2)经预算,购买设备自己不超过117万元,你认为有哪几种购买方案?
(3)在(2)的条件下,若每月要求处理无水不低于2050吨,为节约资金,请你为公司设计一种最省钱的方案.
分析 (1)利用买一台A型比购B型多3万元,买2台A型比购买3台B型少5万元可列二元一次方程组,然后解方程组可得到m、n的值;
(2)设购买污水处理设备A型设备x台,B型设备(10-x)台,利用购买设备自己不超过117万元列不等式14x+11(10-x)≤117,解得x≤$\frac{7}{3}$,然后x取非负整数可得到购买方案;
(3)利用每月要求处理无水不低于2050吨列不等式250x+200(10-x)≥2050,解x≥1,加上x≤$\frac{7}{3}$,则1≤x≤$\frac{7}{3}$,再x取非负整数得到x为1,2,然后比较x=1和x=2的购买资金可得到最省钱的方案.
解答 解:(1)由题意得$\left\{\begin{array}{l}{m-n=3}\\{2m=3n-5}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=14}\\{n=11}\end{array}\right.$;
(2)设购买污水处理设备A型设备x台,B型设备(10-x)台,
根据题意得14x+11(10-x)≤117,解得x≤$\frac{7}{3}$
∵x取非负整数,
∴x=0,1,2,
∴有三种购买方案:
①A型设备0台,B型设备10台;
②A型设备1台,B型设备9台;
③A型设备2台,B型设备8台;
(3)由题意:250x+200(10-x)≥2050,解x≥1,
又∵x≤$\frac{7}{3}$,
∴1≤x≤$\frac{7}{3}$,
而x取非负整数,
∴x为1,2,
当x=1时,购买资金为:14×1+11×9=113(万元),
当x=2时,购买资金为:14×2+11×8=116(万元),
∴为了节约资金,应选购A型设备1台,B型设备9台.
点评 本题考查了一元一次不等式的应用:由实际问题中的不等关系列出不等式,建立解决问题的数学模型,通过解不等式可以得到实际问题的答案.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案| 种植户 | 种植A类蔬菜面积 (亩) | 种植B类蔬菜面积 (单亩) | 总收入 (单位:元) |
| 甲 | 3 | 2 | 28000 |
| 乙 | 2 | 1 | 16500 |
(1)求A、B两类蔬菜每亩平均收入格式多少元?
(2)某种植户准备租18亩地用来种植A、B两类蔬菜,为了使总收入不低于96000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所用租地方案.
| 甲 | 12 | 13 | 14 | 15 | 10 | 16 | 13 | 11 | 15 | 11 |
| 乙 | 11 | 16 | 17 | 14 | 13 | 19 | 6 | 8 | 10 | 16 |
(2)哪种小麦的长势比较整齐?
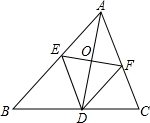 如图,△ABC的∠BAC的平分线AD被EF垂直平分,且E、F分别在AB,AC上,求证:四边形AEDF是菱形.
如图,△ABC的∠BAC的平分线AD被EF垂直平分,且E、F分别在AB,AC上,求证:四边形AEDF是菱形. 如图,已知线段a,b.
如图,已知线段a,b. 已知∠AEM=∠DGN,你能说明AB平行于CD吗?
已知∠AEM=∠DGN,你能说明AB平行于CD吗? 如图:矩形ABCD中,AB=2,BC=5,E、G分别在AD、BC上,且DE=BG=1.
如图:矩形ABCD中,AB=2,BC=5,E、G分别在AD、BC上,且DE=BG=1.