题目内容
3. 如图,已知线段a,b.
如图,已知线段a,b.(1)按下列要求作图:
①用直尺和圆规作Rt△ABC,使∠C=90°,BC=a,AC=b;
②用直尺和圆规作AB边的中垂线,分别交AC,AB于D,E两点,连结BD.
(2)若∠A=38°,求∠CBD的度数;
(3)若a=3,b=4,求DE的长.
分析 (1)①先任作射线,在射线上截取AC=b,接着过点C作AC的垂线,然后在垂线上截取CB=a,从而得到Rt△ABC;
②利用基本作图(作已知线段的垂直平分线)作出DE;
(2)先根据线段垂直平分线的性质定理得到DA=DB,则∠DBA=∠A=38°,再根据三角形外角性质计算出∠CDB,然后利用互余计算∠CBD的度数;
(3)先利用勾股定理得到AB=5,则AE=$\frac{1}{2}$AB=$\frac{5}{2}$,再证明Rt△ADE∽Rt△ABC,然后利用相似比求DE的长.
解答 解:(1)①如图,△ABC为所作;
②如图,BD为所作;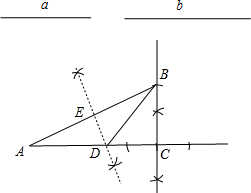
(2)∵DE垂直平分AB,
∴DA=DB,
∴∠DBA=∠A=38°,
∴∠CDB=∠DBA+∠A=76°,
∴∠CBD=90°-76°=14°;
(3)在Rt△ABC中,AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴AE=$\frac{1}{2}$AB=$\frac{5}{2}$,
∵∠EAD=∠CAB,
∴Rt△ADE∽Rt△ABC,
∴DE:BC=AE:AC,即DE:3=$\frac{5}{2}$:4,
∴DE=$\frac{15}{8}$.
点评 本题考查了作图-基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).利用勾股定理和相似比可解决几何计算问题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
15.为了更好治理岳阳河水质,安岳县污水处理公司计划购买10台污水处理设备,现有A、B两种型号的设备,其中每台的价格、月处理污水量如表:
经调查:买一台A型比购B型多3万元,买2台A型比购买3台B型少5万元.
(1)求m,n的值;
(2)经预算,购买设备自己不超过117万元,你认为有哪几种购买方案?
(3)在(2)的条件下,若每月要求处理无水不低于2050吨,为节约资金,请你为公司设计一种最省钱的方案.
| A型 | B型 | |
| 价格(万元/台) | m | n |
| 处理污水量(吨/月) | 250 | 200 |
(1)求m,n的值;
(2)经预算,购买设备自己不超过117万元,你认为有哪几种购买方案?
(3)在(2)的条件下,若每月要求处理无水不低于2050吨,为节约资金,请你为公司设计一种最省钱的方案.

 已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,求证:OE=OF.
已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,求证:OE=OF. 如图,在三角形AOB中,A、O、B三点坐标分别是A(1,5),O(0,0),B(4,2).求三角形AOB的面积.
如图,在三角形AOB中,A、O、B三点坐标分别是A(1,5),O(0,0),B(4,2).求三角形AOB的面积.