题目内容
5．
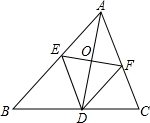如图，△ABC的∠BAC的平分线AD被EF垂直平分，且E、F分别在AB，AC上，求证：四边形AEDF是菱形．
分析 根据角平分线定义可得∠BAD=∠CAD，根据线段垂直平分线的性质可得AE=ED，AF=FD，然后根据等边对等角和等量代换证明∠FAD=∠ADE，∠EAD=∠ADF，从而证明四边形AEDF是平行四边形，再根据对角线互相垂直的平行四边形是菱形可得结论．
解答 证明：∵AD平分∠BAC，
∴∠BAD=∠CAD，
∵EF是AD的垂直平分线，
∴EF⊥AD，AE=ED，AF=FD，
∴∠EAD=∠EDA，∠FAD=∠ADF，
∴∠FAD=∠ADE，∠EAD=∠ADF，
∴AE∥DF，AF∥ED，
∴四边形AEDF是平行四边形，
∵EF⊥AD，
∴四边形AEDF是菱形．
点评 此题主要考查了菱形的判定，关键是掌握对角线互相垂直的平行四边形是菱形．
练习册系列答案
阅读快车系列答案
相关题目
我国水资源比较缺乏，人均水量约为世界人均水量的四分之一，其中西北地区缺水尤为严重．一村民为了蓄水，他把一块矩形白铁皮四个角各切去一个同样大小的小正方形后制作一个无盖水箱用于接雨水．已知白铁皮的长为280cm，宽为160cm（如图）．
如图，在扇形AOB中，∠AOB=120°，弦AB=$2\sqrt{3}$，点M是$\widehat{AB}$上任意一点（与端点A、B不重合），ME⊥AB于点E，以点M为圆心，ME长为半径作⊙M，分别过点A、B作⊙M的切线，两切线相交于点C．
如图，已知直线AB、CD相交于点O，∠DOE=90°，
15．为了更好治理岳阳河水质，安岳县污水处理公司计划购买10台污水处理设备，现有A、B两种型号的设备，其中每台的价格、月处理污水量如表：
经调查：买一台A型比购B型多3万元，买2台A型比购买3台B型少5万元．
（1）求m，n的值；
（2）经预算，购买设备自己不超过117万元，你认为有哪几种购买方案？
（3）在（2）的条件下，若每月要求处理无水不低于2050吨，为节约资金，请你为公司设计一种最省钱的方案．
| A型 | B型 | |
| 价格（万元/台） | m | n |
| 处理污水量（吨/月） | 250 | 200 |
（1）求m，n的值；
（2）经预算，购买设备自己不超过117万元，你认为有哪几种购买方案？
（3）在（2）的条件下，若每月要求处理无水不低于2050吨，为节约资金，请你为公司设计一种最省钱的方案．