题目内容
8.在△ABC中,∠B=40°,∠C=60°,则∠B与∠C的平分线相交夹角(只考虑小于直角的夹角)度数为( )| A. | 50° | B. | 100° | C. | 130° | D. | 150° |
分析 首先根据∠ABC、∠ACB的平分线交于点D,求出∠DBC、∠DCB的度数和是多少;然后在△BCD中,根据三角形的内角和定理,用180°减去∠DBC、∠DCB的度数和,求出∠BDC的度数是多少;最后用180°减去∠BDC的度数,求出∠CDE的度数,即可判断出∠B与∠C的平分线相交夹角度数为多少.
解答 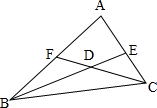 解:如图,∠ABC、∠ACB的平分线交于点D,
解:如图,∠ABC、∠ACB的平分线交于点D,
∵∠ABC、∠ACB的平分线交于点D,
∴∠ABD=∠DBC,∠DCB=∠ACD,
∴∠DBC+∠DCB=(40°+60°)÷2=100°÷2=50°,
∴∠BDC=180°-50°=130°,
∴∠CDE=180°-∠BDC=180°-130°=50°,
即∠B与∠C的平分线相交夹角度数为50°.
故选:A.
点评 (1)此题主要考查了三角形的内角和定理,要熟练掌握,解答此题的关键是要明确:三角形的内角和是180°.
(2)此题还考查了两条直线的夹角,要熟练掌握,解答此题的关键是要明确:两条相交直线的夹角范围为(0°,90°].
(3)此题还考查了角平分线的性质和应用,要熟练掌握,解答此题的关键是要明确:一个角的角平分线把这个角分成两个大小相等的角.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
15.关于x的一元二次方程(m-2)x2+2x+1=0有实数根,则m的取值范围是( )
| A. | m≤3 | B. | m<3 | C. | m<3且m≠2 | D. | m≤3且m≠2 |
 甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题: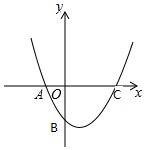 设抛物线y=$\frac{\sqrt{3}}{2}$(x+1)(x-2)与x轴交于A、C两点(点A在点C的左边),与y轴交于点B.
设抛物线y=$\frac{\sqrt{3}}{2}$(x+1)(x-2)与x轴交于A、C两点(点A在点C的左边),与y轴交于点B.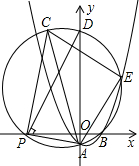 如图,在平面直角坐标系中,抛物线y═$\frac{1}{2}$x2+bx+c经过点A(0,-1),B(2,0)P(t,0)是x轴负半轴上一动点,过点P作PA的垂线交△PAB的外接圆于点C,△PAB的外接圆与y轴交于点D,与抛物线在第一象限限交于点E.
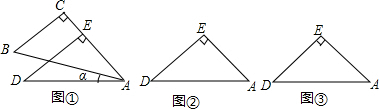
如图,在平面直角坐标系中,抛物线y═$\frac{1}{2}$x2+bx+c经过点A(0,-1),B(2,0)P(t,0)是x轴负半轴上一动点,过点P作PA的垂线交△PAB的外接圆于点C,△PAB的外接圆与y轴交于点D,与抛物线在第一象限限交于点E.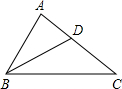 如图,在△ABC中,BD平分∠ABC,∠A=2∠C.
如图,在△ABC中,BD平分∠ABC,∠A=2∠C.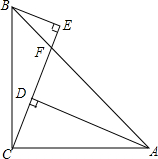 如图,AD=CE=24,BC=25,BE∥AD.BF:AF=7:24,给出下列结论:
如图,AD=CE=24,BC=25,BE∥AD.BF:AF=7:24,给出下列结论: