题目内容
3. 甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:(1)甲登山的速度是每分钟10米,乙在A地提速时距地面的高度b为30米;
(2)若乙提速后,乙的速度是甲登山速度的3倍,请分别求出甲、乙二人登山全过程中,登山时距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,乙追上了甲?
分析 (1)甲的速度=(300-100)÷20=10,根据图象知道一分的时间,走了15米,然后即可求出A地提速时距地面的高度;
(2)乙提速后,乙的速度是甲登山速度的3倍,所以乙的速度是30米/分.那么求出点B的坐标,加上点A的坐标代入一次函数解析式即可求出乙的函数解析式,把C、D坐标代入一次函数解析式可求出甲的函数解析式;
(3)由(2)AB、CD的解析式建立二元一次方程组,求出方程组的解就求出了以追上甲的时间.
解答 解:(1)甲的速度为:(300-100)÷20=10米/分,
根据图中信息知道乙一分的时间,走了15米,
那么2分时,将走30米,
∴b=30,
故答案为:10,30.
(2)由图知:x=$\frac{300-30}{30}$+2=11,
设CD的解析式为:y=k1x+b1,
∵C(0,100),D(20,300)
∴$\left\{\begin{array}{l}{{b}_{1}=100}\\{20{k}_{1}+{b}_{1}=300}\end{array}\right.$
解得:$\left\{\begin{array}{l}{{k}_{1}=10}\\{{b}_{1}=100}\end{array}\right.$
∴线段CD的解析式:y甲=10x+100(0≤x≤20);
当0≤x≤2时,y乙=15x;
当2≤x≤11时,设直线AB的解析式为:y=k2x+b2
∵A(2,30),B(11,300),
∴$\left\{\begin{array}{l}{2{k}_{2}+{b}_{2}=30}\\{11{k}_{2}+{b}_{2}=300}\end{array}\right.$
解得:$\left\{\begin{array}{l}{{k}_{2}=30}\\{{b}_{2}=-30}\end{array}\right.$
∴y=30x-30,
∴折线OAB的解析式为:${y}_{乙}=\left\{\begin{array}{l}{15x(0≤x≤2)}\\{30x-30(2≤x≤11)}\end{array}\right.$;
(3)由$\left\{\begin{array}{l}{y=30x-30}\\{y=10x+100}\end{array}\right.$
解得:$\left\{\begin{array}{l}{x=6.5}\\{y=165}\end{array}\right.$,
∴登山6.5分钟时乙追上甲.
点评 本题是一道一次函数的综合试题,考查了行程问题中路程=速度×时间的关系变化的运用,待定系数法求一次函数的解析式的运用,图象的交点坐标的求法.在解答中注意线段的解析式要确定自变量的取值范围.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案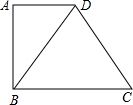 如图,已知直角梯形ABCD的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形ABCD的中位线长为( )
如图,已知直角梯形ABCD的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形ABCD的中位线长为( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 10cm |
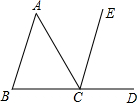 如图,能判断AB∥CE的条件是( )
如图,能判断AB∥CE的条件是( )| A. | ∠A=∠ACE | B. | ∠A=∠ECD | C. | ∠B=∠BCA | D. | ∠B=∠ACE |
| A. | 50° | B. | 100° | C. | 130° | D. | 150° |
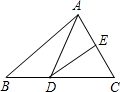 如图,△ABC的周长为21cm,将△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边于点E,连接AD,若AE=3cm,则△ABD的周长是( )
如图,△ABC的周长为21cm,将△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边于点E,连接AD,若AE=3cm,则△ABD的周长是( )| A. | 15cm | B. | 18cm | C. | 21cm | D. | 24cm |
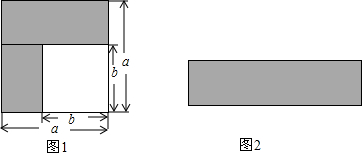
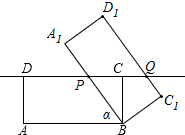 已知矩形ABCD,AB=8,BC=4,将它绕着点B按顺时针方向旋转α度(0<α≤180)得到矩形A1BC1D1,此时A1B,C1D1这两边所在的直线分别与CD边所在的直线相交于点P、Q,当DP:DQ=1:2时,DP的长为5或1+$\sqrt{11}$.
已知矩形ABCD,AB=8,BC=4,将它绕着点B按顺时针方向旋转α度(0<α≤180)得到矩形A1BC1D1,此时A1B,C1D1这两边所在的直线分别与CD边所在的直线相交于点P、Q,当DP:DQ=1:2时,DP的长为5或1+$\sqrt{11}$.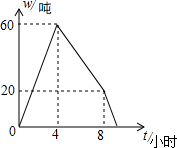 某仓库调拨一批物资,调进物资共用8小时,调进物资4小时后同时开始调出物资(调进与调出物资的速度均保持不变).该仓库库存物资w(吨)与时间t(小时)之间的关系如图所示,求这批物资从开始调进到全部调出所需要的时间.
某仓库调拨一批物资,调进物资共用8小时,调进物资4小时后同时开始调出物资(调进与调出物资的速度均保持不变).该仓库库存物资w(吨)与时间t(小时)之间的关系如图所示,求这批物资从开始调进到全部调出所需要的时间.