题目内容
20.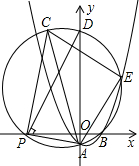 如图,在平面直角坐标系中,抛物线y═$\frac{1}{2}$x2+bx+c经过点A(0,-1),B(2,0)P(t,0)是x轴负半轴上一动点,过点P作PA的垂线交△PAB的外接圆于点C,△PAB的外接圆与y轴交于点D,与抛物线在第一象限限交于点E.
如图,在平面直角坐标系中,抛物线y═$\frac{1}{2}$x2+bx+c经过点A(0,-1),B(2,0)P(t,0)是x轴负半轴上一动点,过点P作PA的垂线交△PAB的外接圆于点C,△PAB的外接圆与y轴交于点D,与抛物线在第一象限限交于点E.(1)求抛物线的解析式;
(2)当△PAB的外接圆的圆心落在y轴上时,求该圆的半径;
(3)用含t的式子表示C、D的坐标.
分析 (1)把A、B两点的坐标代入可求得b、c的值,可求得抛物线的解析式;
(2)由条件可知PA=PB,可求得P点坐标,由勾股定理可求得半径;
(3)可先证明△AOB∽△APC,可求得$\frac{AP}{PC}$=$\frac{1}{2}$,过P作y轴的平行线,分别过A、C作其垂线,垂足分别为G、F,则AG=-t,GP=1,可用t表示出PF、CF,可求得C点坐标,又结合条件可证明∠CDA=90°,可表示出D点坐标.
解答 解:(1)把A(0,-1),B(2,0)代入y=$\frac{1}{2}$x2+bx+c,
可得$\left\{\begin{array}{l}{-1=c}\\{0=2+2b+c}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-\frac{1}{2}}\\{c=-1}\end{array}\right.$.
∴抛物线解析式为y=$\frac{1}{2}$x2-$\frac{1}{2}$x-1;
(2)当△PAB的外接圆的圆心落在y轴上时,AP=AB,此时P(-2,0),
设圆的半径为r,则(r-1)2+22=r2,
解得r=2.5;
(3)∵∠ACP=∠ABP,且∠AOB=90°=∠APC,
∴△AOB∽△APC,
∴$\frac{AP}{AO}$=$\frac{PC}{OB}$,即$\frac{AP}{PC}$=$\frac{1}{2}$,
∵∠APC=90°,
∴∠APG+∠CPF=∠CPF+∠PCF=90°,
∴∠APG=∠PCF,且∠AGP=∠CFP,
∴△APG∽△PCF,
∴$\frac{AG}{PF}$=$\frac{PG}{CF}$=$\frac{AP}{PC}$=$\frac{1}{2}$,
如图,过P作y轴的平行线,分别过A、C作其垂线,垂足分别为G、F,则AG=-t,GP=1,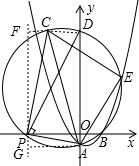
∴PF=-2t,CF=2,
∴C(2+t,-2t),
连接CD,
∵∠APC=90°,
∴AC为直径,
∴∠CDA=90°,
∴D(0,-2t).
点评 本题主要考查二次函数的综合应用,涉及待定系数法、相似三角形的判定和性质、圆周角定理等知识点.在(1)中注意待定系数法应用的步骤,在(2)中注意垂径定理的应用,在(3)中,注意圆周角定理的应用.本题考查知识较为基础,难度不大.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,能判断AB∥CE的条件是( )
如图,能判断AB∥CE的条件是( )| A. | ∠A=∠ACE | B. | ∠A=∠ECD | C. | ∠B=∠BCA | D. | ∠B=∠ACE |
| A. | 50° | B. | 100° | C. | 130° | D. | 150° |
 观察下列各个等式:12=1,12+22=5,12+22+32=14,12+22+32+42=30,….
观察下列各个等式:12=1,12+22=5,12+22+32=14,12+22+32+42=30,….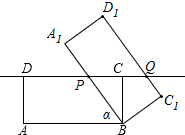 已知矩形ABCD,AB=8,BC=4,将它绕着点B按顺时针方向旋转α度(0<α≤180)得到矩形A1BC1D1,此时A1B,C1D1这两边所在的直线分别与CD边所在的直线相交于点P、Q,当DP:DQ=1:2时,DP的长为5或1+$\sqrt{11}$.
已知矩形ABCD,AB=8,BC=4,将它绕着点B按顺时针方向旋转α度(0<α≤180)得到矩形A1BC1D1,此时A1B,C1D1这两边所在的直线分别与CD边所在的直线相交于点P、Q,当DP:DQ=1:2时,DP的长为5或1+$\sqrt{11}$.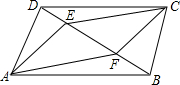 如图,己知AB∥DC,且AB=CD,BF=DE,说明AE∥CF,AF∥CE的理由.
如图,己知AB∥DC,且AB=CD,BF=DE,说明AE∥CF,AF∥CE的理由.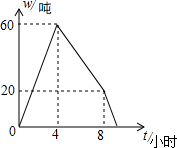 某仓库调拨一批物资,调进物资共用8小时,调进物资4小时后同时开始调出物资(调进与调出物资的速度均保持不变).该仓库库存物资w(吨)与时间t(小时)之间的关系如图所示,求这批物资从开始调进到全部调出所需要的时间.
某仓库调拨一批物资,调进物资共用8小时,调进物资4小时后同时开始调出物资(调进与调出物资的速度均保持不变).该仓库库存物资w(吨)与时间t(小时)之间的关系如图所示,求这批物资从开始调进到全部调出所需要的时间.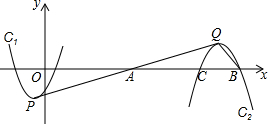 如图,抛物线C1:y=x2+2x-3的顶点为P,将该抛物线绕点A(a,0)(a>0)旋转180°后得到的抛物线C2,抛物线C2的顶点为Q,与x轴的交点是B、C,点B在点C的右侧.若∠PQB=90°,则a=7.
如图,抛物线C1:y=x2+2x-3的顶点为P,将该抛物线绕点A(a,0)(a>0)旋转180°后得到的抛物线C2,抛物线C2的顶点为Q,与x轴的交点是B、C,点B在点C的右侧.若∠PQB=90°,则a=7. 如图,在?ABCD中,点E在AD上,若DE=6,S△DEF:S△BCF=4:25,则AE=9.
如图,在?ABCD中,点E在AD上,若DE=6,S△DEF:S△BCF=4:25,则AE=9.