题目内容
19.若一个多边形的内角和的度数恰好与外角和的度数相等,则这个多边形的边数为4.分析 根据多边形的内角和公式与多边形的外角和的度数结合题意,列出方程,解方程即可求解.
解答 解:设这个多边形的边数为n,
根据题意,得(n-2)•180°=360°,
解得,n=4.
故答案为:4.
点评 本题考查的是代表性的内角和外角的知识,掌握多边形内角和的计算公式:(n-2)×180°和多边形的外角和是360°是解题的关键.

练习册系列答案
相关题目
14.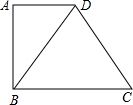 如图,已知直角梯形ABCD的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形ABCD的中位线长为( )
如图,已知直角梯形ABCD的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形ABCD的中位线长为( )
 如图,已知直角梯形ABCD的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形ABCD的中位线长为( )
如图,已知直角梯形ABCD的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形ABCD的中位线长为( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 10cm |
11.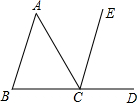 如图,能判断AB∥CE的条件是( )
如图,能判断AB∥CE的条件是( )
 如图,能判断AB∥CE的条件是( )
如图,能判断AB∥CE的条件是( )| A. | ∠A=∠ACE | B. | ∠A=∠ECD | C. | ∠B=∠BCA | D. | ∠B=∠ACE |
8.在△ABC中,∠B=40°,∠C=60°,则∠B与∠C的平分线相交夹角(只考虑小于直角的夹角)度数为( )
| A. | 50° | B. | 100° | C. | 130° | D. | 150° |
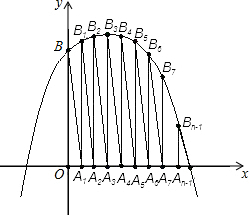 观察下列各个等式:12=1,12+22=5,12+22+32=14,12+22+32+42=30,….
观察下列各个等式:12=1,12+22=5,12+22+32=14,12+22+32+42=30,….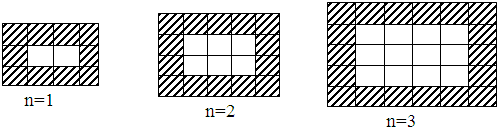
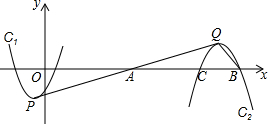 如图,抛物线C1:y=x2+2x-3的顶点为P,将该抛物线绕点A(a,0)(a>0)旋转180°后得到的抛物线C2,抛物线C2的顶点为Q,与x轴的交点是B、C,点B在点C的右侧.若∠PQB=90°,则a=7.
如图,抛物线C1:y=x2+2x-3的顶点为P,将该抛物线绕点A(a,0)(a>0)旋转180°后得到的抛物线C2,抛物线C2的顶点为Q,与x轴的交点是B、C,点B在点C的右侧.若∠PQB=90°,则a=7.