题目内容
关于x的一元二次方程x2+2kx+k-1=0
(1)求证:方程x2+2kx+k-1=0有两个不相等的实数根;
(2)若方程x2+2kx+k-1=0有且只有一个根的绝对值小于2,求k的取值范围.
(1)求证:方程x2+2kx+k-1=0有两个不相等的实数根;
(2)若方程x2+2kx+k-1=0有且只有一个根的绝对值小于2,求k的取值范围.
考点:根的判别式,抛物线与x轴的交点
专题:
分析:(1)先计算判别式得到△=(2k)2-4(k-1),再根据非负数的性质得到△>0,然后根据判别式的意义即可得到结论;
(2)根据抛物线与x轴的交点得到抛物线y=x2+2kx+k-1与y轴的交点在x轴下方,且抛物线与x轴的一个交点在(-2,0)和点(2,0)之间,则x=-2时,y<0,即4-4k+k-1<0;x=2时,4+4k+k-1>0;然后求出三个不等式解的公共部分即可.
(2)根据抛物线与x轴的交点得到抛物线y=x2+2kx+k-1与y轴的交点在x轴下方,且抛物线与x轴的一个交点在(-2,0)和点(2,0)之间,则x=-2时,y<0,即4-4k+k-1<0;x=2时,4+4k+k-1>0;然后求出三个不等式解的公共部分即可.
解答:解:(1)△=(2k)2-4(k-1)=(2k-1)2+3,
∵(2k-1)2≥0,
∴(2k-1)2+3>0,
∴方程x2+2kx+k-1=0有两个不相等的实数根.
(2)∵方程x2+2kx+k-1=0有且只有一个根的绝对值小于2,
∴抛物线y=x2+2kx+k-1与y轴的交点在x轴下方,且抛物线与x轴的一个交点在(-2,0)和点(2,0)之间,
x=-2时,y<0,即4-4k+k-1<0,解得k>1,
x=2时,y>0,即4+4k+k-1>0,解得k>-
,
抛物线y=x2+2kx+k-1与y轴的交点在x轴上方,且抛物线与x轴的一个交点在(-2,0)和点(2,0)之间,
x=-2时,y<0,即4-4k+k-1>0,解得k<1,
x=2时,y>0,即4+4k+k-1<0,解得k<-
,
∴k的范围为k>1或k<-
.
∵(2k-1)2≥0,
∴(2k-1)2+3>0,
∴方程x2+2kx+k-1=0有两个不相等的实数根.
(2)∵方程x2+2kx+k-1=0有且只有一个根的绝对值小于2,
∴抛物线y=x2+2kx+k-1与y轴的交点在x轴下方,且抛物线与x轴的一个交点在(-2,0)和点(2,0)之间,
x=-2时,y<0,即4-4k+k-1<0,解得k>1,
x=2时,y>0,即4+4k+k-1>0,解得k>-
| 3 |
| 5 |
抛物线y=x2+2kx+k-1与y轴的交点在x轴上方,且抛物线与x轴的一个交点在(-2,0)和点(2,0)之间,
x=-2时,y<0,即4-4k+k-1>0,解得k<1,
x=2时,y>0,即4+4k+k-1<0,解得k<-
| 3 |
| 5 |
∴k的范围为k>1或k<-
| 3 |
| 5 |
点评:此题考查根的判别式与一元二次方程与二次函数的关系,以及配方法的运用与非负数的性质,理解题意,正确利用函数解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
每天早上7点45分我们开始第一节课,此时钟表上分针与时针的夹角是( )
| A、60° | B、45° |
| C、37.5° | D、35.° |
 一架外国侦察机沿ED方向侵入我国领空进行非法侦察,我空军的战斗机沿AC方向与外国侦察机平行飞行,进行跟踪监视,我机在A处与外国侦察机B处的距离为50米,∠CAB为30°,这时外国侦察机突然转向,以偏左45°的方向飞行,我机继续沿AC方向以400米/秒的速度飞行,外国侦察机在C点故意撞击我战斗机,使我战斗机受损.问外国侦察机由B到C的速度是多少?(结果保留整数,参考数据
一架外国侦察机沿ED方向侵入我国领空进行非法侦察,我空军的战斗机沿AC方向与外国侦察机平行飞行,进行跟踪监视,我机在A处与外国侦察机B处的距离为50米,∠CAB为30°,这时外国侦察机突然转向,以偏左45°的方向飞行,我机继续沿AC方向以400米/秒的速度飞行,外国侦察机在C点故意撞击我战斗机,使我战斗机受损.问外国侦察机由B到C的速度是多少?(结果保留整数,参考数据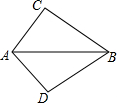 如图,已知∠ACB=∠ADB=90°,欲说明BC=BD,可补充条件
如图,已知∠ACB=∠ADB=90°,欲说明BC=BD,可补充条件