题目内容
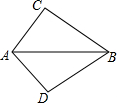 如图,已知∠ACB=∠ADB=90°,欲说明BC=BD,可补充条件
如图,已知∠ACB=∠ADB=90°,欲说明BC=BD,可补充条件考点:全等三角形的判定与性质
专题:开放型
分析:此题是一道开放型的题目,答案不唯一,如AC=AD或∠CAB=∠DAB或∠CBA=∠DBA.
解答:解:AC=AD,
理由是:∵∠ACB=∠ADB=90°,
在Rt△ACB和Rt△ADB中,
,
∴Rt△ACB≌Rt△ADB(HL),
∴BC=BD.
故答案为:AC=AD.
理由是:∵∠ACB=∠ADB=90°,
在Rt△ACB和Rt△ADB中,
|
∴Rt△ACB≌Rt△ADB(HL),
∴BC=BD.
故答案为:AC=AD.
点评:本题考查了全等三角形的性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,HL等,全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
若x≠y,则下列不能成立的等式是( )
| A、(x-y)2 =(y-x)2 |
| B、(x-y)3 =-(y-x)3 |
| C、(x+y)2 =(-x-y)2 |
| D、(x+y)2 =(-x+y)2 |
已知⊙O的半径是5,点A到圆心O的距离是7,则点A与⊙O的位置关系是( )
| A、点A在⊙O上 |
| B、点A在⊙O内 |
| C、点A在⊙O外 |
| D、点A与圆心O重合 |
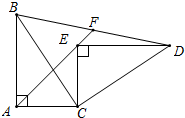 如图所示,Rt△ABC≌Rt△CED,∠BAC=∠CED=90°,延长AE到BD交与点F,求证:BF=FD.
如图所示,Rt△ABC≌Rt△CED,∠BAC=∠CED=90°,延长AE到BD交与点F,求证:BF=FD. 已知,AB是⊙O的直径,AD、BC是⊙O的切线,AB=4,AD=3,BC=6.
已知,AB是⊙O的直径,AD、BC是⊙O的切线,AB=4,AD=3,BC=6. 在△ABC中,AB=AC,点D在BC边上,且BD=AD,AB+AD=BC,求∠B的度数.
在△ABC中,AB=AC,点D在BC边上,且BD=AD,AB+AD=BC,求∠B的度数.