题目内容
 一架外国侦察机沿ED方向侵入我国领空进行非法侦察,我空军的战斗机沿AC方向与外国侦察机平行飞行,进行跟踪监视,我机在A处与外国侦察机B处的距离为50米,∠CAB为30°,这时外国侦察机突然转向,以偏左45°的方向飞行,我机继续沿AC方向以400米/秒的速度飞行,外国侦察机在C点故意撞击我战斗机,使我战斗机受损.问外国侦察机由B到C的速度是多少?(结果保留整数,参考数据
一架外国侦察机沿ED方向侵入我国领空进行非法侦察,我空军的战斗机沿AC方向与外国侦察机平行飞行,进行跟踪监视,我机在A处与外国侦察机B处的距离为50米,∠CAB为30°,这时外国侦察机突然转向,以偏左45°的方向飞行,我机继续沿AC方向以400米/秒的速度飞行,外国侦察机在C点故意撞击我战斗机,使我战斗机受损.问外国侦察机由B到C的速度是多少?(结果保留整数,参考数据| 2 |
| 3 |
考点:解直角三角形的应用-方向角问题
专题:
分析:过点B作BF⊥AC于点F,根据题意得出BC,FC,AF的长,进而利用速度与路程之间的关系得出答案.
解答: 解:过点B作BF⊥AC于点F,
解:过点B作BF⊥AC于点F,
∵∠CBD=45°,
∴∠CBF=∠C=45°,
∵∠A=30°,AB=50,
∴BF=25m,AF=25
m,
∴FC=25m,则BC=25
m,
∴AC=25
+25≈68(m),
68÷400≈0.17(秒),
故25
÷0.17≈208(m/s),
答:外国侦察机由B到C的速度是208m/s.
 解:过点B作BF⊥AC于点F,
解:过点B作BF⊥AC于点F,∵∠CBD=45°,
∴∠CBF=∠C=45°,
∵∠A=30°,AB=50,
∴BF=25m,AF=25
| 3 |
∴FC=25m,则BC=25
| 2 |
∴AC=25
| 3 |
68÷400≈0.17(秒),
故25
| 2 |
答:外国侦察机由B到C的速度是208m/s.
点评:此题主要考查了解直角三角形的应用,根据题意得出AC,BC的长是解题关键.

练习册系列答案
相关题目
若3a2m+1b2和a3b2n-2是同类项,则
+
的值是( )
| 1 |
| m |
| 2 |
| n |
| A、2 | B、3 | C、4 | D、5 |
 教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-
教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-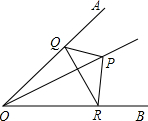 如图,∠AOB=45°,角内有一点P,PO=10,在角两边上有两点Q、R(均不同于点O),则△PQR的周长最小值是
如图,∠AOB=45°,角内有一点P,PO=10,在角两边上有两点Q、R(均不同于点O),则△PQR的周长最小值是