题目内容
2014年巴西世界杯决赛的票价分别为一等席990美元、二等席660美元、三等席440美元.某公司组织体育比赛获奖的20名职员到巴西观看2014年世界杯的决赛,除去其他费用,计划购买两种门票,恰好用完11000美元.你能设计出几种方案供该公司选择?请说明理由.
考点:二元一次方程的应用
专题:
分析:此题分三种情况讨论:可以设一等席和二等席或一等席和三等席或二等席和三等席.然后根据解应是正整数进行分析其解.
解答:解:①设购买一等席门票x张,二等席门票(20-x)张,根据题意可列方程为:
990x+660(20-x)=11000,
解得:x=-
,
因为x、y都是正整数,
所以此方案不可行.
②设购买一等席门票x张,三等席门票(20-x)张,根据题意可列方程:
990x+440(20-x)=11000
解得:x=4,
则20-x=16.
所以可购买一等席门票,4张,三等席门票16张.
③设购买二等席门票x张,三等席门票(20-x)张,根据题意可列方程:
660x+440(20-x)=11000
解得:x=10,
则20-x=10,
所以可购买二等席门票10张,三等席门票10张.
答:共有两种购票方案,购一等席门票4张,三等席门票16张,或购二等席门票10张,三等席门票10张.
990x+660(20-x)=11000,
解得:x=-
| 220 |
| 33 |
因为x、y都是正整数,
所以此方案不可行.
②设购买一等席门票x张,三等席门票(20-x)张,根据题意可列方程:
990x+440(20-x)=11000
解得:x=4,
则20-x=16.
所以可购买一等席门票,4张,三等席门票16张.
③设购买二等席门票x张,三等席门票(20-x)张,根据题意可列方程:
660x+440(20-x)=11000
解得:x=10,
则20-x=10,
所以可购买二等席门票10张,三等席门票10张.
答:共有两种购票方案,购一等席门票4张,三等席门票16张,或购二等席门票10张,三等席门票10张.
点评:此题主要考查了二元一次方程的应用,要能够分情况列出二元一次方程,根据它们的解必须是正整数进行分析讨论.

练习册系列答案
相关题目
 正方体的六个面分别标有1,2,3,4,5,6六个数字,如图是其三种不同的放置方式,与数字“6”相对的面上的数字是( )
正方体的六个面分别标有1,2,3,4,5,6六个数字,如图是其三种不同的放置方式,与数字“6”相对的面上的数字是( ) 教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-
教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-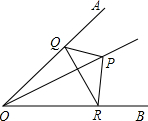 如图,∠AOB=45°,角内有一点P,PO=10,在角两边上有两点Q、R(均不同于点O),则△PQR的周长最小值是
如图,∠AOB=45°,角内有一点P,PO=10,在角两边上有两点Q、R(均不同于点O),则△PQR的周长最小值是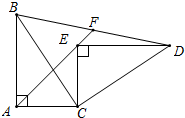 如图所示,Rt△ABC≌Rt△CED,∠BAC=∠CED=90°,延长AE到BD交与点F,求证:BF=FD.
如图所示,Rt△ABC≌Rt△CED,∠BAC=∠CED=90°,延长AE到BD交与点F,求证:BF=FD.