题目内容
14.如图,抛物线y=ax2+bx-4与x轴交于点A(-2,0)、B(4,0),与y轴交于点C,过点C作x轴的平行线交抛物线于点D,连接AC,作直线BC.(1)求抛物线y=ax2+bx-4的表达式;
(2)如图2,点E(x,0)是线段OB上的一点,过点E作与x轴垂直的直线与直线BC交于点F,与抛物线交于点G.
①线段FG的长是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;
②连接CG,当∠DCG=∠ACO时,求点G的坐;
(3)若点P是直线BC下方的抛物线上的一点,点Q在y轴上,点M在线段BC上,当以C,P,Q,M为顶点的四边形是菱形时,直接写出菱形的边长.
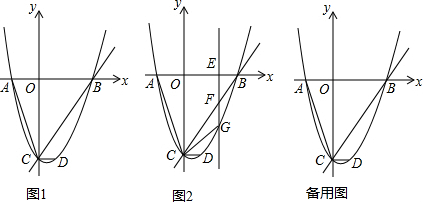
分析 (1)先求得点C的坐标,设抛物线的解析式为y=a(x+2)(x-4),将点C的坐标代入求得a的值即可;
(2)①先求得直线CB的解析式,由F(x,x-4),G(x,$\frac{1}{2}$x2-x-4)得到FG=-$\frac{1}{2}$x2+2x,然后依据二次函数的性质求解即可;②过点D作DH∥y轴,交CG于点H,先求得点D的坐标,则可得到CD的长,然后证明$\frac{HD}{CD}$=$\frac{AO}{OC}$=$\frac{1}{2}$,可得到点H的坐标,再求得CG的解析式,最后求得CG与抛物线的交点坐标即可;(3)当点Q在点C的上方时,由菱形的对角线平分每一组对角可得到∠ACP=90°,则CP∥x轴,可求得点P的坐标,故此可得到菱形的边长;当点Q在点C的下方时.过点P作PE⊥y轴,垂足为E.设菱形CQPM的边长为a,可求得点P的坐标为($\frac{\sqrt{2}}{2}$a,-4-a+$\frac{\sqrt{2}}{2}$a),将点P的坐标代入抛物线的解析式可求得a的值.
解答 解:(1)将x=0代入抛物线的解析式得:y=-4,
∴C(0,-4).
设抛物线的解析式为y=a(x+2)(x-4),将点C的坐标代入得:-8a=-4,解得:a=$\frac{1}{2}$,
∴y=$\frac{1}{2}$(x+2)(x-4),即y=$\frac{1}{2}$x2-x-4.
(2)①设直线BC的解析式为y=kx+b,将点B和点C的坐标代入得:$\left\{\begin{array}{l}{b=-4}\\{4k+b=0}\end{array}\right.$,
解得:k=1,b=-4.
∴直线CB的解析式为y=x-4.
∵点E(x,0),EF⊥x轴,
∴F(x,x-4),G(x,$\frac{1}{2}$x2-x-4).
∴FG=x-4-($\frac{1}{2}$x2-x-4)=-$\frac{1}{2}$x2+2x,
∴当x=-$\frac{2}{-\frac{1}{2}×2}$=2时,FG有最大值,FG的最大值=2.
②如图1所示:过点D作DH∥y轴,交CG于点H.
∵CD∥x轴,
∴点D的纵坐标为-4.
将y=-4代入抛物线的解析式得:-4=$\frac{1}{2}$x2-x-4,解得:x=2或x=0,
∴D(2,-4).
∴CD=2.
∵∠ACO=∠DCG,
∴tan∠ACO=tan∠DCG,
∴$\frac{HD}{CD}$=$\frac{AO}{OC}$=$\frac{1}{2}$即$\frac{DH}{2}$=$\frac{1}{2}$,解得DH=1.
∴H(2,-3).
设CG的解析式为y=kx-4,将点H的坐标代入得:2k-4=-3,解得k=$\frac{1}{2}$,
∴直线CG的解析式为y=$\frac{1}{2}$x-4.
将y=$\frac{1}{2}$x-4代入y=$\frac{1}{2}$x2-x-4得:$\frac{1}{2}$x-4=$\frac{1}{2}$x2-x-4,解得:x=0或x=3,
将x=3代入y=$\frac{1}{2}$x-4得:y=-$\frac{5}{2}$.
∴G(3,-$\frac{5}{2}$).
(3)如图2所示,当点Q在点C的上方时.
∵OB=OC=4,
∴∠OCB=45°.
∵QCPM为菱形,
∴∠ACP=90°.
∴CP∥x轴.
由(2)可知点P的坐标为(2,0).
∴菱形的边长为2.
如图3所示:当点Q在点C的下方时.过点P作PE⊥y轴,垂足为E.
设菱形CQPM的边长为a,则∠QC=PQ=a.
∵∠CQP=45°,
∴EP=QE=$\frac{\sqrt{2}}{2}$a.
∴P的坐标为($\frac{\sqrt{2}}{2}$a,-4-a+$\frac{\sqrt{2}}{2}$a).
将点P的坐标代入抛物线的解析式得:-4-a+$\frac{\sqrt{2}}{2}$a=$\frac{1}{2}$×($\frac{\sqrt{2}}{2}$a)2-$\frac{\sqrt{2}}{2}$a-4,
解得:a=4$\sqrt{2}$-4.
综上所述菱形CQPM的边长为2或4$\sqrt{2}$-4.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式,二次函数的性质、锐角三角函数的定义,菱形的性质,分类讨论是解答本题的关键.

| A. | $\frac{2}{a}$+$\frac{3}{b}$=$\frac{5}{ab}$ | B. | $\frac{3}{3a+b}$=$\frac{1}{a+b}$ | C. | $\frac{ab}{ab-{b}^{2}}$=$\frac{a}{a-b}$ | D. | $\frac{a}{-a+b}$=-$\frac{a}{a+b}$ |
| A. | 这个球可能是白球 | |
| B. | 摸到黑球、白球的可能性的大小一样 | |
| C. | 这个球一定是黑球 | |
| D. | 事先能确定摸到什么颜色的球 |
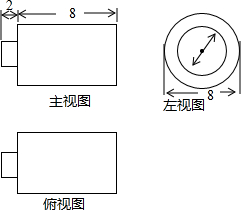 如图,是某几何体的三视图,根据图中所标的数据求得该几何体的体积为( )
如图,是某几何体的三视图,根据图中所标的数据求得该几何体的体积为( )| A. | 120π | B. | 132π | C. | 136π | D. | 236π |
| 身高(cm) | 172 | 173 | 175 | 176 |
| 人数(个) | 2 | 7 | 3 | 4 |
| A. | 174cm,173cm | B. | 173cm,174cm | C. | 174cm,174cm | D. | 174cm,175cm |
 如图,已知AB⊥CD,EF⊥AB,∠DGC=105°,∠BCA=75°,请说明∠CEF+∠CDG=180°的理由.
如图,已知AB⊥CD,EF⊥AB,∠DGC=105°,∠BCA=75°,请说明∠CEF+∠CDG=180°的理由.
 将△ABC的纸片按如图所示的方式折叠,使点B落在边AC上,记为点B′,折叠痕为EF,已知AB=AC=8,BC=10,若以点B′、F、C为顶点的三角形与△ABC相似,那么BF的长度是$\frac{40}{9}$或5.
将△ABC的纸片按如图所示的方式折叠,使点B落在边AC上,记为点B′,折叠痕为EF,已知AB=AC=8,BC=10,若以点B′、F、C为顶点的三角形与△ABC相似,那么BF的长度是$\frac{40}{9}$或5.