题目内容
5.下列等式成立的是( )| A. | $\frac{2}{a}$+$\frac{3}{b}$=$\frac{5}{ab}$ | B. | $\frac{3}{3a+b}$=$\frac{1}{a+b}$ | C. | $\frac{ab}{ab-{b}^{2}}$=$\frac{a}{a-b}$ | D. | $\frac{a}{-a+b}$=-$\frac{a}{a+b}$ |
分析 各项计算得到结果,即可作出判断.
解答 解:A、原式=$\frac{3a+2b}{ab}$,不符合题意;
B、原式为最简结果,不符合题意;
C、原式=$\frac{ab}{b(a-b)}$=$\frac{a}{a-b}$,符合题意;
D、原式=-$\frac{a}{a-b}$,不符合题意,
故选C
点评 此题考查了分式的加减法,以及分式的基本性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.一个正常成年人行走时的步长大约是( )
| A. | 0.5cm | B. | 50cm | C. | 5m | D. | 50m |
16. 如右图所示的工件的主视图是( )
如右图所示的工件的主视图是( )
 如右图所示的工件的主视图是( )
如右图所示的工件的主视图是( )| A. |  | B. |  | C. |  | D. |  |
20.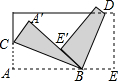 将一长方形纸片,按图中的方式折叠,BC、BD为折痕,折叠后点E′刚好落在A′B上,则∠CBD的度数为( )
将一长方形纸片,按图中的方式折叠,BC、BD为折痕,折叠后点E′刚好落在A′B上,则∠CBD的度数为( )
 将一长方形纸片,按图中的方式折叠,BC、BD为折痕,折叠后点E′刚好落在A′B上,则∠CBD的度数为( )
将一长方形纸片,按图中的方式折叠,BC、BD为折痕,折叠后点E′刚好落在A′B上,则∠CBD的度数为( )| A. | 60° | B. | 75° | C. | 90° | D. | 95° |
15.下列等式由左边至右边的变形中,属于因式分解的是( )
| A. | x2+3x-1=x(x+3)-1 | B. | x2-9+2x=(x+3)(x-3)+2x | ||
| C. | a2-16=(a+4)(a-4) | D. | (x+2)(x-2)=x2-4 |
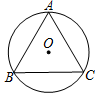 若⊙O是等边△ABC的外接圆,⊙O的半径为2,则等边△ABC的边长为$2\sqrt{3}$.
若⊙O是等边△ABC的外接圆,⊙O的半径为2,则等边△ABC的边长为$2\sqrt{3}$.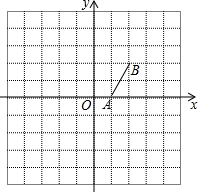 如图,在正方形网格中,每个小正方形的边长为1个单位长度.平面直角坐标系xOy的原点O在格点上,x轴、y轴都在网格线上,线段A、B在格点上.
如图,在正方形网格中,每个小正方形的边长为1个单位长度.平面直角坐标系xOy的原点O在格点上,x轴、y轴都在网格线上,线段A、B在格点上.