题目内容
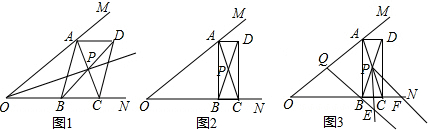
9.操作与探究:如图1,在锐角∠MON的边OM、ON上分别取点A、C,使OA=OC,在OC上取点B,作?ABCD,连接AC、BD交于点P,作射线OP.(1)求证:OP平分∠MON.
(2)移动点B使∠BPC=∠MON,求证:?ABCD是矩形.
(3)如图3,在(2)的条件下,去OA中点Q连接QB,将∠BPC绕点P逆时针旋转适当的角度,得到∠EPF(点E、F分别是∠EPF的两边与QB的延长线、ON的交点).猜想线段PE与PF之间的数量关系,并证明你的结论.
分析 (1)根据SSS判定△AOP≌△COP,即可得到∠AOP=∠COP,进而得出结论:OP平分∠MON;
(2)根据三角形内角和可得∠PBC=∠OAC,再根据等边对等角可得∠OAC=∠OCA,根据等角对等边可得PB=PC,再根据对角线相等的平行四边形是矩形,即可判定?ABCD是矩形;
(3)根据旋转的性质,可设∠BPC=∠EPF=α,根据等腰△BCP内角和为180°,可得∠PBC=90°-$\frac{1}{2}$α,根据直角三角形斜边上中线的性质,可得∠PBE=90°+$\frac{1}{2}$α,进而得出∠PCF=∠PBE,再由旋转的性质可得∠BPE=∠CPF,最后根据ASA即可判定△PBE≌△PCF,进而得到线段PE与PF之间的数量关系.
解答 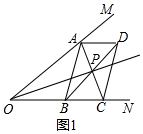 解:(1)∵四边形ABCD是平行四边形,
解:(1)∵四边形ABCD是平行四边形,
∴AP=CP,
在△AOP和△COP中,
$\left\{\begin{array}{l}{OA=OC}\\{OP=OP}\\{AP=CP}\end{array}\right.$,
∴△AOP≌△COP(SSS),
∴∠AOP=∠COP,
∴OP平分∠MON;
(2)证明:∵∠BPC=∠MON,∠BCP=∠ACO,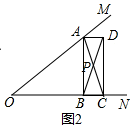
∴∠PBC=∠OAC,
又∵OA=OC,
∴∠OAC=∠OCA,
∴∠PBC=∠PCB,
∴PB=PC,
又∵AC=2PC,BD=2PB,
∴AC=DB,
又∵四边形ABCD是平行四边形,
∴?ABCD是矩形;
(3)线段PE与PF之间的数量关系为:PE=PF.
证明:根据旋转的性质,可设∠BPC=∠EPF=α,则
等腰△BCP中,∠PBC=$\frac{180°-α}{2}$=90°-$\frac{1}{2}$α,
∴∠PCF=∠BPC+∠PBC=α+90°-$\frac{1}{2}$α=90°+$\frac{1}{2}$α,
∵∠ABO=90°,Q为AO的中点,
∴Rt△AOB中,BQ=$\frac{1}{2}$AO=OQ,
∴∠O=∠QBO=∠EBC,
又∵∠BPC=∠MON=α,
∴∠EBC=α,
∴∠PBE=∠PBC+∠EBC=90°-$\frac{1}{2}$α+α=90°+$\frac{1}{2}$α,
∴∠PCF=∠PBE,
由旋转可得,∠BPC=∠EPF,
∴∠BPE=∠CPF,
在△PBE和△PCF中,
$\left\{\begin{array}{l}{∠BPE=∠CPF}\\{BP=CP}\\{∠PCF=∠PBE}\end{array}\right.$,
∴△PBE≌△PCF(ASA),
∴PE=PF.
点评 本题属于四边形综合题,主要考查了平行四边形的性质,矩形的判定,等腰三角形的性质以及全等三角形判定与性质的综合应用,解决问题的关键是掌握:三条边分别对应相等的两个三角形全等;两角及其夹边分别对应相等的两个三角形全等.解题时注意:对角线相等的平行四边形是矩形.

| A. | (2,-2) | B. | (-1,0) | C. | (1,9) | D. | (0,-2) |
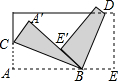 将一长方形纸片,按图中的方式折叠,BC、BD为折痕,折叠后点E′刚好落在A′B上,则∠CBD的度数为( )
将一长方形纸片,按图中的方式折叠,BC、BD为折痕,折叠后点E′刚好落在A′B上,则∠CBD的度数为( )| A. | 60° | B. | 75° | C. | 90° | D. | 95° |
| A. | a=3 | B. | a<3 | C. | a>3 | D. | a≠3 |
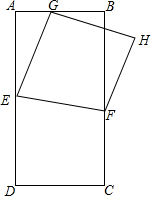 矩形ABCD满足BC=2AB,E、F分别为AD、BC边上的动点,连接EF,沿EF将四边形DEFC翻折至四边形GEFH,点G落在AB上.
矩形ABCD满足BC=2AB,E、F分别为AD、BC边上的动点,连接EF,沿EF将四边形DEFC翻折至四边形GEFH,点G落在AB上.