题目内容
3.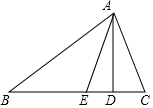 如图,已知△ABC中,AD⊥BC于D,AE为∠BAC的平分线,且∠B=37°,∠C=67°,求∠DAE的度数.
如图,已知△ABC中,AD⊥BC于D,AE为∠BAC的平分线,且∠B=37°,∠C=67°,求∠DAE的度数.
分析 利用三角形的内角和等于180°列式求出∠BAC,根据角平分线的定义求出∠BAE,再根据直角三角形两锐角互余求出∠BAD,然后根据∠DAE=∠BAD-∠BAE计算即可得解.
解答 解:根据三角形的内角和定理得,∠BAC=180°-∠B-∠C=180°-37°-67°=76°,
∴AE为∠BAC的平分线,
∴∠BAE=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×76°=38°,
∵AD⊥BC于D,
∴∠ADB=90°,
∴∠BAD=90°-∠B=90°-37°=53°,
∴∠DAE=∠BAD-∠BAE=53°-38°=15°.
点评 本题考查了三角形的内角和定理,角平分线的定义,直角三角形两锐角互余的性质,熟记定理并准确识图理清图中各角度之间的关系是解题的关键.

练习册系列答案
相关题目
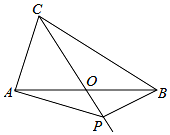 如图,在△ABC中,AB=BC=6,AO=BO,P是射线CO上在AB下方的一个动点,∠AOC=45°.则当△PAB为直角三角形时,AP的长为$\sqrt{18+9\sqrt{2}}$或=$\sqrt{18-9\sqrt{2}}$或3$\sqrt{5}$.
如图,在△ABC中,AB=BC=6,AO=BO,P是射线CO上在AB下方的一个动点,∠AOC=45°.则当△PAB为直角三角形时,AP的长为$\sqrt{18+9\sqrt{2}}$或=$\sqrt{18-9\sqrt{2}}$或3$\sqrt{5}$.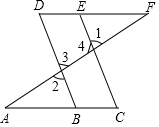 如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证DF∥AC.
如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证DF∥AC.