题目内容
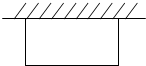 如图,某农场要建一个长方形的养鸡场,鸡场的一边靠墙,墙长25米,另外三边用木栏围着,木栏长40米.
如图,某农场要建一个长方形的养鸡场,鸡场的一边靠墙,墙长25米,另外三边用木栏围着,木栏长40米.(1)若养鸡场面积为150平米,求鸡场靠墙的一边长.
(2)养鸡场面积能否达到250平米?若能,请写出方案;若不能,说明理由.
(3)请设计一方案使得鸡场面积最大.
考点:一元二次方程的应用,二次函数的应用
专题:几何图形问题
分析:(1)长边靠墙,设出鸡场宽为x米,则长(40-2x)米;或宽边靠墙,设出鸡场长为x米,宽为(40-2x)米,然后根据矩形的面积=长×宽,用未知数表示出鸡场的面积,根据面积为200m2,可得方程,解方程即可;
(2)要求鸡场的面积能否达到250平方米,只需让鸡场的面积先等于250,然后看得出的一元二次方程有没有解,如果有就证明可以达到250平方米,如果方程无实数根,说明不能达到250平方米;
(3)直接利用配方法求出二次函数最值即可.
(2)要求鸡场的面积能否达到250平方米,只需让鸡场的面积先等于250,然后看得出的一元二次方程有没有解,如果有就证明可以达到250平方米,如果方程无实数根,说明不能达到250平方米;
(3)直接利用配方法求出二次函数最值即可.
解答:解:(1)长边靠墙,设宽为x米,长为(40-2x)米,根据题意得:
x(40-2x)=150,
-2x2+40x-150=0,
解得:x1=5,x2=15(不合题意舍去),
则鸡场靠墙的一边长为:40-2x=30(不合题意舍去),
宽边靠墙,设长为x米,宽为(40-2x)米,根据题意得:
x(40-2x)=150,
-2x2+40x-150=0,
解得:x1=5(不合题意舍去),x2=15,
则鸡场靠墙的一边长为:40-2x=10.
答:鸡场靠墙的一边长10米.
(2)根据题意得:x(40-2x)=250,
∴-2x2+40x-250=0,
∵b2-4ac=402-4×(-2)×(-250)<0,
∴方程无实数根,
∴不能使鸡场的面积能达到250m2;
(3)设总面积为y,则y=x(40-2x)=-2x2+40x=-2(x-10)2+200,
则当x=10米时,y最大=200平方米.
x(40-2x)=150,
-2x2+40x-150=0,
解得:x1=5,x2=15(不合题意舍去),
则鸡场靠墙的一边长为:40-2x=30(不合题意舍去),
宽边靠墙,设长为x米,宽为(40-2x)米,根据题意得:
x(40-2x)=150,
-2x2+40x-150=0,
解得:x1=5(不合题意舍去),x2=15,
则鸡场靠墙的一边长为:40-2x=10.
答:鸡场靠墙的一边长10米.
(2)根据题意得:x(40-2x)=250,
∴-2x2+40x-250=0,
∵b2-4ac=402-4×(-2)×(-250)<0,
∴方程无实数根,
∴不能使鸡场的面积能达到250m2;
(3)设总面积为y,则y=x(40-2x)=-2x2+40x=-2(x-10)2+200,
则当x=10米时,y最大=200平方米.
点评:此题主要考查了一元二次方程的应用以及二次函数最值求法等知识,熟记一元二次方程根与系数的关系.读懂题意,找到等量关系准确的列出方程是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
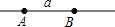 如图,下列说法正确的是( )
如图,下列说法正确的是( )| A、直线AB和直线a不是同一条直线 |
| B、直线AB和直线BA是两条直线 |
| C、射线AB和射线BA是两条射线 |
| D、线段AB和线段BA是两条线段 |
 某住宅小区在住宅建设时留下一块448平方米的矩形ABCD空地,准备建一个底面是矩形的喷水池,设计如图所示,喷水池底面的长是宽的2倍,在喷水池的前侧留一块5米宽的空地,其它三侧各保留2米宽的道路及1米宽的绿化带.
某住宅小区在住宅建设时留下一块448平方米的矩形ABCD空地,准备建一个底面是矩形的喷水池,设计如图所示,喷水池底面的长是宽的2倍,在喷水池的前侧留一块5米宽的空地,其它三侧各保留2米宽的道路及1米宽的绿化带. 如图,长方形OABC在平面直角坐标系xOy的第一象限内,点A在x轴正半轴上,点C在y轴的正半轴上,点D、E分别是OC、BC的中点,∠CDE=30°,点E的坐标为(2,a).
如图,长方形OABC在平面直角坐标系xOy的第一象限内,点A在x轴正半轴上,点C在y轴的正半轴上,点D、E分别是OC、BC的中点,∠CDE=30°,点E的坐标为(2,a).