题目内容
10.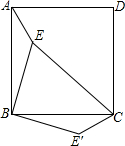 如图,E是正方形ABCD内一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE’的位置.若AE=I,BE=2,CE=3,则么BE′C=135°.
如图,E是正方形ABCD内一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE’的位置.若AE=I,BE=2,CE=3,则么BE′C=135°.
分析 首先根据旋转的性质得出,△EBE′是直角三角形,进而得出∠BEE′=∠BE′E=45°,即可得出答案.
解答 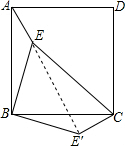 解:连接EE′
解:连接EE′
∵△ABE绕点B顺时针旋转90°到△CBE′
∴∠EBE′是直角,
∴△EBE′是直角三角形,
∵△ABE与△CE′B全等,
∴BE=BE′=2,∠AEB=∠BE′C,
∴∠BEE′=∠BE′E=45°,
∵EE′2=22+22=8,AE=CE′=1,EC=3,
∴EC2=E′C2+EE′2,
∴△EE′C是直角三角形,
∴∠EE′C=90°,
∴∠AEB=135°.
故答案为:135.
点评 此题主要考查了旋转的性质,根据已知得出△EBE′是直角三角形是解题关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
1. 如图,利用直尺和三角尺作平行线,其依据是( )
如图,利用直尺和三角尺作平行线,其依据是( )
 如图,利用直尺和三角尺作平行线,其依据是( )
如图,利用直尺和三角尺作平行线,其依据是( )| A. | 同位角相等,两直线平行 | B. | 内错角相等,两直线平行 | ||
| C. | 同旁内角互补,两直线平行 | D. | 两直线平行,同位角相等 |
5.下列运算结果正确的是( )
| A. | $\frac{a}{b}$÷$\frac{c}{d}$=$\frac{ac}{bd}$ | B. | $\frac{b}{a-b}$+$\frac{a}{b-a}$=1 | ||
| C. | ($\frac{2a}{a-b}$)2=$\frac{4{a}^{2}}{{a}^{2}-{b}^{2}}$ | D. | $\frac{{m}^{4}}{{n}^{5}}$•$\frac{{n}^{4}}{{m}^{3}}$=$\frac{m}{n}$ |
2.已知|a+1|+$\sqrt{7+b}$=0,则a+b=( )
| A. | -8 | B. | -6 | C. | 6 | D. | 8 |
19.二次三项式3x2-2x-6的值为3,则x2-$\frac{2}{3}$x+6的值为( )
| A. | 18 | B. | 12 | C. | 9 | D. | 7 |