题目内容
1.若a+b=0,a≠b,则$\frac{b}{a}$(a-1)+$\frac{a}{b}$(b-1)的值为-2.分析 先把原式进行化简,再把a+b=0代入进行计算即可.
解答 解:∵a+b=0,a≠b,
∴原式=b-$\frac{b}{a}$+a-$\frac{a}{b}$
=(a+b)-($\frac{b}{a}$+$\frac{a}{b}$)
=0-$\frac{{b}^{2}+{a}^{2}}{ab}$
=-$\frac{(a+b)^{2}-2ab}{ab}$
=-$\frac{{0}^{2}-2ab}{ab}$
=-2.
故答案为:-2.
点评 本题考查的是分式的化简求值,分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.

练习册系列答案
相关题目
5.下列方程组中,是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{3{x}^{2}+y=1}\\{10x-8y=-9}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-y=2}\\{\frac{1}{x}-3y=-\frac{7}{4}}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x=1}\\{2x-y=6}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{xy=4}\\{x+2y=6}\end{array}\right.$ |
 时,则二次根式
时,则二次根式 的值为_________。
的值为_________。 如图,在?ABCD中,AB=8cm,BC=12cm,∠BCD的平分线交AD于点M,则AM=4cm.
如图,在?ABCD中,AB=8cm,BC=12cm,∠BCD的平分线交AD于点M,则AM=4cm. ×3
×3 =6
=6 B.
B.  +
+ =
=
 -2
-2 =3
=3 D.
D.  ÷
÷ =
=
 ②
② ③
③ ④
④ 中,一元二次方程的个数是( )
中,一元二次方程的个数是( )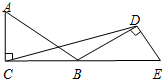 如图,△ABC绕着顶点B顺时针旋转150°得△EBD,连结CD,若∠ACB=90°,∠ABC=30°,则∠BDC的度数是15°.
如图,△ABC绕着顶点B顺时针旋转150°得△EBD,连结CD,若∠ACB=90°,∠ABC=30°,则∠BDC的度数是15°.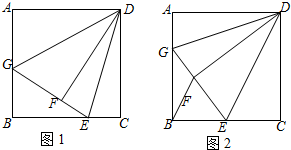
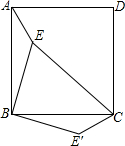 如图,E是正方形ABCD内一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE’的位置.若AE=I,BE=2,CE=3,则么BE′C=135°.
如图,E是正方形ABCD内一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE’的位置.若AE=I,BE=2,CE=3,则么BE′C=135°.