题目内容
18.若直角三角形的两直角边的长分别为a、b,且满足$\sqrt{a-3}$+(b-4)2=0,则该直角三角形的斜边长为5.分析 直接利用偶次方的性质以及二次根式的性质得出a,b的值,再利用勾股定理得出斜边长.
解答 解:∵$\sqrt{a-3}$+(b-4)2=0,
∴a=3,b=4,
∴该直角三角形的斜边长为:$\sqrt{{3}^{2}+{4}^{2}}$=5.
故答案为:5.
点评 此题主要考查了勾股定理以及偶次方的性质和二次根式的性质,正确得出a,b的值是解题关键.

练习册系列答案
相关题目
13.下列数据不能确定物体位置的是( )
| A. | 2楼4号 | B. | 大学路19号 | C. | 北偏东60° | D. | 东经111°北纬40° |
3.已知(x-2y-1)2+|2x+y-7|=0,则3x-y=( )
| A. | 3 | B. | 1 | C. | 8 | D. | -6 |
7. “奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.从A地到D地的距离是( )
“奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.从A地到D地的距离是( )
 “奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.从A地到D地的距离是( )
“奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.从A地到D地的距离是( )| A. | 30$\sqrt{3}$m | B. | 20$\sqrt{5}$m | C. | 30$\sqrt{2}$m | D. | 15$\sqrt{6}$m |
 ×3
×3 =6
=6 B.
B.  +
+ =
=
 -2
-2 =3
=3 D.
D.  ÷
÷ =
=
 某市有A、B、C、D四个大型超市,分别位于一条东西走向的平安大路两侧,如图,若C(-2,8)、D(0,0),请建立适当的直角坐标系,并写出A、B两个超市相应的坐标.
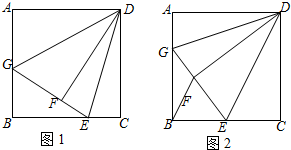
某市有A、B、C、D四个大型超市,分别位于一条东西走向的平安大路两侧,如图,若C(-2,8)、D(0,0),请建立适当的直角坐标系,并写出A、B两个超市相应的坐标.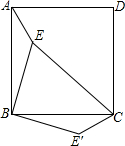 如图,E是正方形ABCD内一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE’的位置.若AE=I,BE=2,CE=3,则么BE′C=135°.
如图,E是正方形ABCD内一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE’的位置.若AE=I,BE=2,CE=3,则么BE′C=135°.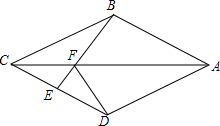 如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.
如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.