题目内容
 某长方体包装盒的展开图如图,包装盒的表面积为146cm2.
某长方体包装盒的展开图如图,包装盒的表面积为146cm2.(1)若设包装盒的高为x,试用含x的表达式表示包装盒的长和宽;
(2)求这个包装盒的体积.
考点:一元二次方程的应用
专题:几何图形问题
分析:先根据表面积求出长方体的高,再根据长方体的体积公式计算出其值就可以了.
解答:解:(1)设高为xcm,则长为(13-2x)cm,宽为
(14-2x)cm.
(2)由题意,得
[(13-2x)
(14-2x)+
(14-2x)x+x(13-2x)]×2=146,
解得:x1=2,x2=-9(舍去)
∴长为:13-2x=9cm,宽为:5cm.
长方体的体积为:9×5×2=90cm3.
答:这个包装盒的体积为90cm3.
| 1 |
| 2 |
(2)由题意,得
[(13-2x)
| 1 |
| 2 |
| 1 |
| 2 |
解得:x1=2,x2=-9(舍去)
∴长为:13-2x=9cm,宽为:5cm.
长方体的体积为:9×5×2=90cm3.
答:这个包装盒的体积为90cm3.
点评:本题考查了列一元二次方程解实际问题的运用,一元二次方程的额解法的运用,几何体的表面积的运用,几何体的体积公式的运用.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
下列方程中,一元二次方程共( )
①3x2+x=20;②x2+y2=5;③x2-
=4;④x2=1;⑤x2-
+3=0.
①3x2+x=20;②x2+y2=5;③x2-
| 1 |
| x |
| x |
| 3 |
| A、5个 | B、4个 | C、3个 | D、2个 |
 已知直线y=
已知直线y=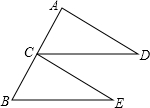 如图,C是线段AB的中点,CD∥BE,且CD=BE,求证:AD=CE.
如图,C是线段AB的中点,CD∥BE,且CD=BE,求证:AD=CE. 在如图所示的4×3网格中,每个小正方形的边长均为1,正方形顶点叫格点,连结两个网格格点的线段叫网格线段.点A固定在格点上.
在如图所示的4×3网格中,每个小正方形的边长均为1,正方形顶点叫格点,连结两个网格格点的线段叫网格线段.点A固定在格点上.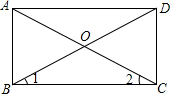 如图,四边形ABCD是平行四边形,AC,BD相交于点O,且∠1=∠2.
如图,四边形ABCD是平行四边形,AC,BD相交于点O,且∠1=∠2.