题目内容
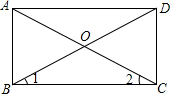 如图,四边形ABCD是平行四边形,AC,BD相交于点O,且∠1=∠2.
如图,四边形ABCD是平行四边形,AC,BD相交于点O,且∠1=∠2.(1)求证:四边形ABCD是矩形;
(2)若∠AOB=60°,AB=8,求BC的长.
考点:矩形的判定,平行四边形的性质
专题:
分析:(1)由“对角线相等的平行四边形是矩形”进行证明;
(2)利用矩形的性质推知∠1=∠2=30°,通过解直角△ABC来求BC的长度.
(2)利用矩形的性质推知∠1=∠2=30°,通过解直角△ABC来求BC的长度.
解答: (1)证明:如图,∵四边形ABCD是平行四边形,
(1)证明:如图,∵四边形ABCD是平行四边形,
∴OC=
AC,OB=
BD.
又∵∠1=∠2,
∴OB=OC,
∴BD=AC,
∴?ABCD是矩形;
(2)∵由(1)知,?ABCD是矩形,
∴∠ABC=90°,
又∵∠AOB=60°,
∴∠1=30°,
∴∠2=30°,
∴BC=AB•cot30°=8
.即BC的长度是8
.
 (1)证明:如图,∵四边形ABCD是平行四边形,
(1)证明:如图,∵四边形ABCD是平行四边形,∴OC=
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠1=∠2,
∴OB=OC,
∴BD=AC,
∴?ABCD是矩形;
(2)∵由(1)知,?ABCD是矩形,
∴∠ABC=90°,
又∵∠AOB=60°,
∴∠1=30°,
∴∠2=30°,
∴BC=AB•cot30°=8
| 3 |
| 3 |
点评:本题考查了矩形的判定与平行四边形的性质.此题利用了“平行四边形的对角线相互平分”和“对角线相等的平行四边形是矩形”来证明平行四边形ABCD是矩形的.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 某长方体包装盒的展开图如图,包装盒的表面积为146cm2.
某长方体包装盒的展开图如图,包装盒的表面积为146cm2. 如图,直线y=kx-2与x轴交于点A(1,0),与y轴交于点B,若直线AB上的点C在第三象限,且S△BOC=3,求点C的坐标.
如图,直线y=kx-2与x轴交于点A(1,0),与y轴交于点B,若直线AB上的点C在第三象限,且S△BOC=3,求点C的坐标.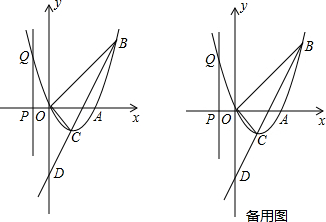
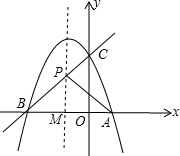 如图,已知二次函数y=ax2+bx+3(a≠0)的图象与x轴交于点A(1,0)、B(-3,0),与y轴交于点C.
如图,已知二次函数y=ax2+bx+3(a≠0)的图象与x轴交于点A(1,0)、B(-3,0),与y轴交于点C.