题目内容
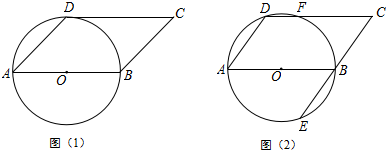
17. 如图,⊙O是△ABC的外接圆,AC是直径,点E是AB的中点,延长EO交⊙O于D点,若BC=DC,AB=2$\sqrt{3}$,求$\widehat{AD}$的长度.
如图,⊙O是△ABC的外接圆,AC是直径,点E是AB的中点,延长EO交⊙O于D点,若BC=DC,AB=2$\sqrt{3}$,求$\widehat{AD}$的长度.
分析 连结BD,如图,利用圆心角、弧、弦的关系,由BC=DC得$\widehat{BC}$=$\widehat{DC}$,则根据垂径定理得到AC垂直平分BD,所以AB=AD,同样可得DA=DB,则可判断△ABD为等边三角形,所以∠BAC=30°,∠ABD=60°,根据圆周角定理得∠AOD=2∠ABD=120°,然后在Rt△AEO中计算出AO,最后利用弧长公式计算即可.
解答 解:连结BD,如图,
∵BC=DC,
∴$\widehat{BC}$=$\widehat{DC}$,
∴AC垂直平分BD,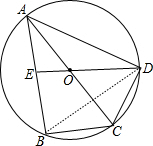
∴AB=AD,
∵点E是AB的中点,即AE=BE=$\sqrt{3}$,
∴DE⊥AB,
∴DA=DB,
∴AB=AD=DB,
∴△ABD为等边三角形,
∴∠BAC=30°,∠ABD=60°,
∴∠AOD=2∠ABD=120°,
在Rt△AEO中,∵∠EAO=30°,
∴OE=$\frac{\sqrt{3}}{3}$AE=1,AO=2OE=2,
∴$\widehat{AD}$的长度=$\frac{120•π•2}{180}$=$\frac{4π}{3}$.
点评 本题考查了三角形的外接圆与外心:三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.解决本题的关键是证明△ABD为等边三角形.

练习册系列答案
相关题目
5.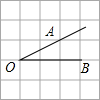 如图,将∠AOB放在边长为1的小正方形组成的网格中,则sin∠AOB的值为( )
如图,将∠AOB放在边长为1的小正方形组成的网格中,则sin∠AOB的值为( )
 如图,将∠AOB放在边长为1的小正方形组成的网格中,则sin∠AOB的值为( )
如图,将∠AOB放在边长为1的小正方形组成的网格中,则sin∠AOB的值为( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
6. 如图,已知直线AB∥CD,∠C=125°,∠E=80°,那么∠A的大小为( )
如图,已知直线AB∥CD,∠C=125°,∠E=80°,那么∠A的大小为( )
 如图,已知直线AB∥CD,∠C=125°,∠E=80°,那么∠A的大小为( )
如图,已知直线AB∥CD,∠C=125°,∠E=80°,那么∠A的大小为( )| A. | 40° | B. | 45° | C. | 50° | D. | 80° |
7. 如图,点A是过点(1,4)的双曲线y=$\frac{k}{x}$上第一象限内的任意一点,AB⊥x轴,垂足为B,点C是x轴上点B右侧的任意一点,点D是线段AC的中点,直线BD交y轴于点E,则△BCE的面积为( )
如图,点A是过点(1,4)的双曲线y=$\frac{k}{x}$上第一象限内的任意一点,AB⊥x轴,垂足为B,点C是x轴上点B右侧的任意一点,点D是线段AC的中点,直线BD交y轴于点E,则△BCE的面积为( )
 如图,点A是过点(1,4)的双曲线y=$\frac{k}{x}$上第一象限内的任意一点,AB⊥x轴,垂足为B,点C是x轴上点B右侧的任意一点,点D是线段AC的中点,直线BD交y轴于点E,则△BCE的面积为( )
如图,点A是过点(1,4)的双曲线y=$\frac{k}{x}$上第一象限内的任意一点,AB⊥x轴,垂足为B,点C是x轴上点B右侧的任意一点,点D是线段AC的中点,直线BD交y轴于点E,则△BCE的面积为( )| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
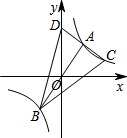 如图,在平面直角坐标系xOy中,直线y=$\frac{3}{2}$x与双曲线y=$\frac{k}{x}$相交于A、B两点,且A点横坐标为2,C是第一象限内双曲线上一点,连接CA并延长交y轴于点D,连接BD,BC.
如图,在平面直角坐标系xOy中,直线y=$\frac{3}{2}$x与双曲线y=$\frac{k}{x}$相交于A、B两点,且A点横坐标为2,C是第一象限内双曲线上一点,连接CA并延长交y轴于点D,连接BD,BC.