题目内容
7. 如图,点A是过点(1,4)的双曲线y=$\frac{k}{x}$上第一象限内的任意一点,AB⊥x轴,垂足为B,点C是x轴上点B右侧的任意一点,点D是线段AC的中点,直线BD交y轴于点E,则△BCE的面积为( )
如图,点A是过点(1,4)的双曲线y=$\frac{k}{x}$上第一象限内的任意一点,AB⊥x轴,垂足为B,点C是x轴上点B右侧的任意一点,点D是线段AC的中点,直线BD交y轴于点E,则△BCE的面积为( )| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
分析 由点(1,4)在双曲线上,可求出k=4,根据点D为AC的中点可得出S△EAD=S△ECD、S△BAD=S△BCD,进而可得出S△BCE=S△BAE,再根据△ABE和△ABO同底等高利用反比例系数k的几何意义即可得出S△BCE=S△BAE=S△ABO=$\frac{1}{2}$|k|=2,此题得解.
解答 解:连接AE、AO,如图所示.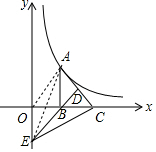
∵点(1,4)在双曲线y=$\frac{k}{x}$的图象上,
∴k=1×4=4,
∴双曲线的解析式为y=$\frac{4}{x}$.
∵点D为AC的中点,
∴S△EAD=S△ECD,S△BAD=S△BCD,
∴S△BCE=S△BAE.
∵△ABE和△ABO同底等高,
∴S△BCE=S△BAE=S△ABO=$\frac{1}{2}$|k|=2.
故选B.
点评 本题考查了反比例函数数与一次函数的交点问题以及反比例函数系数k的几何意义,根据三角形间的关系找出S△BCE=S△BAE=S△ABO=$\frac{1}{2}$|k|是解题的关键.

练习册系列答案
相关题目
2.根据我国《环境空气质量指数AQI技术规定》(试行),AQI共分0-50,51-100,101-150,151-200,201-300和大于300六级,指数越大,级别越高,说明污染越严重,对人体健康的影响也越明显.专家建议:当空气质量指数小于150时,可以户外运动;空气质量指数151及以上,不适合进行旅游等户外运动,如表是某市未来10天的空气质量指数预测:
(1)该市市民在这10天内随机选取1天进行户外运动,求这10天该市市民不适合户外运动的概率;
(2)一名外地游客计划在这10天内到该市旅游,随机选取连续2天游玩,求这10天中适合他旅游的概率.
| 时间 | 11日 | 12日 | 13日 | 14日 | 15日 | 16日 | 17日 | 18日 | 19日 | 20日 |
| AQ1 | 149 | 143 | 251 | 254 | 138 | 55 | 69 | 102 | 243 | 269 |
(2)一名外地游客计划在这10天内到该市旅游,随机选取连续2天游玩,求这10天中适合他旅游的概率.
12.在下列二次根式的化简中,被开方数与$\sqrt{2}$的被开方数相同的是( )
| A. | $\sqrt{20}$ | B. | $\sqrt{4}$ | C. | $\sqrt{8}$ | D. | $\sqrt{12}$ |
 如图,⊙O是△ABC的外接圆,AC是直径,点E是AB的中点,延长EO交⊙O于D点,若BC=DC,AB=2$\sqrt{3}$,求$\widehat{AD}$的长度.
如图,⊙O是△ABC的外接圆,AC是直径,点E是AB的中点,延长EO交⊙O于D点,若BC=DC,AB=2$\sqrt{3}$,求$\widehat{AD}$的长度.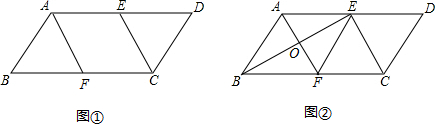
 尺规作图:已知⊙O及⊙O上一点A,如图.
尺规作图:已知⊙O及⊙O上一点A,如图.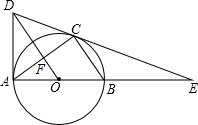 如图,AB为⊙O的直径,点C在⊙O上,连接BC、AC,作OD∥BC,与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
如图,AB为⊙O的直径,点C在⊙O上,连接BC、AC,作OD∥BC,与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.