题目内容
16.函数y=kxm-1+3(k≠0)是一次函数,试求方程$\frac{3}{x+3}=\frac{m}{x+1}$的解.分析 根据一次函数的定义求得m的值;然后将其代入所求的方程,并解分式方程,并检验.
解答 解:依题意得:m-1=1,
解得m=2,
所以$\frac{3}{x+3}=\frac{2}{x+1}$,
整理,得
3x+3=2x+6,
解得x=3,
经检验,x=3是原方程的解.
点评 本题考查了一次函数的定义和解分式方程.解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
7.已知圆上均匀分布着2000个点,从中均等地选出A、B、C、D四个不同的点,则弦AB与CD相交的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
11.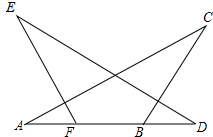 如图,AF=DB,∠A=∠D,添加一个条件,使△ABC≌△DFE,添加的条件不能为( )
如图,AF=DB,∠A=∠D,添加一个条件,使△ABC≌△DFE,添加的条件不能为( )
 如图,AF=DB,∠A=∠D,添加一个条件,使△ABC≌△DFE,添加的条件不能为( )
如图,AF=DB,∠A=∠D,添加一个条件,使△ABC≌△DFE,添加的条件不能为( )| A. | AC=DE | B. | EF=BC | C. | ∠AFE=∠DBC | D. | ∠E=∠C |
5.若不等式组$\left\{\begin{array}{l}{x-b≤0}\\{x+a>0}\end{array}\right.$的解集为2<x≤3,则a,b的值分别为( )
| A. | -2,3 | B. | 2,-3 | C. | 3,-2 | D. | -3,2 |
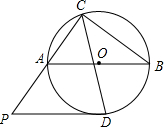 如图,△ABC内接于⊙O,且AB为⊙O的直径,过CA延长线上点P作⊙O的切线PD.切点为D,且PD∥AB.
如图,△ABC内接于⊙O,且AB为⊙O的直径,过CA延长线上点P作⊙O的切线PD.切点为D,且PD∥AB.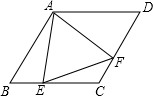 如图,在菱形ABCD中,∠B=60°,若AB=2,点E是BC边上一动点,∠EAF=60°,AF交CD于点F
如图,在菱形ABCD中,∠B=60°,若AB=2,点E是BC边上一动点,∠EAF=60°,AF交CD于点F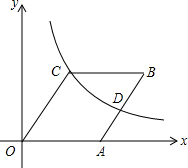 如图,在菱形OABC中点A在x轴的正半轴上,点B坐标为(8,4)双曲线y=$\frac{k}{x}$(k>0)经过点C,交AB于点D.
如图,在菱形OABC中点A在x轴的正半轴上,点B坐标为(8,4)双曲线y=$\frac{k}{x}$(k>0)经过点C,交AB于点D.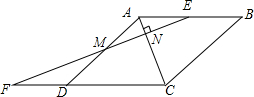 如图,四边形ABCD是菱形,点E为AB的中点,延长CD至F,使得DF=$\frac{1}{2}$CD,连接EF分别交AD,AC于点M,N.
如图,四边形ABCD是菱形,点E为AB的中点,延长CD至F,使得DF=$\frac{1}{2}$CD,连接EF分别交AD,AC于点M,N.