题目内容
19. 矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),点D是OA的中点,点E在线段AB上,当△CDE的周长最小时,求点E的坐标.
矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),点D是OA的中点,点E在线段AB上,当△CDE的周长最小时,求点E的坐标.
分析 如图,作点D关于直线AB的对称点H,连接CH与AB的交点为E,此时△CDE的周长最小,先求出直线CH解析式,再求出直线CH与AB的交点即可解决问题.
解答 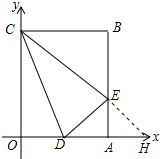 解:如图,作点D关于直线AB的对称点H,连接CH与AB的交点为E,此时△CDE的周长最小.
解:如图,作点D关于直线AB的对称点H,连接CH与AB的交点为E,此时△CDE的周长最小.
∵D($\frac{3}{2}$,0),A(3,0),
∴H($\frac{9}{2}$,0),
∴直线CH解析式为y=-$\frac{8}{9}$x+4,
∴x=3时,y=$\frac{4}{3}$,
∴点E坐标(3,$\frac{4}{3}$).
点评 本题考查矩形的性质、坐标与图形的性质、轴对称-最短问题、一次函数等知识,解题的关键是利用轴对称找到点E位置,学会利用一次函数解决交点问题,属于中考常考题型.

练习册系列答案
相关题目
7.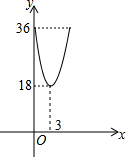 已知两个正方形的面积和y与其中一个正方形边长x之间的函数解析式y=ax2-12x+36的图象如图所示,(3,18)是该图象的顶点,当x=4时,这两个正方形的面积和为( )
已知两个正方形的面积和y与其中一个正方形边长x之间的函数解析式y=ax2-12x+36的图象如图所示,(3,18)是该图象的顶点,当x=4时,这两个正方形的面积和为( )
 已知两个正方形的面积和y与其中一个正方形边长x之间的函数解析式y=ax2-12x+36的图象如图所示,(3,18)是该图象的顶点,当x=4时,这两个正方形的面积和为( )
已知两个正方形的面积和y与其中一个正方形边长x之间的函数解析式y=ax2-12x+36的图象如图所示,(3,18)是该图象的顶点,当x=4时,这两个正方形的面积和为( )| A. | 19 | B. | 20 | C. | 22 | D. | 24 |
4.适合|2a+5|+|2a-3|=8的整数a的值有( )
| A. | 4个 | B. | 5个 | C. | 7个 | D. | 9个 |
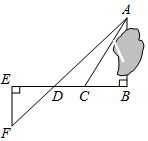 为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于点D,C在BD上,有四位同学分别测量出以下四组数据:①BC,∠ACB;②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A、B间距离的有( )
为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于点D,C在BD上,有四位同学分别测量出以下四组数据:①BC,∠ACB;②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A、B间距离的有( )
 如图,连结正五边形的各条对角线AD,AC,BE,BD,CE,给出下列结论:①∠AME=108°;②五边形PFQNM∽五边形ABCDE;③AN2=AM•AD,其中正确的是( )
如图,连结正五边形的各条对角线AD,AC,BE,BD,CE,给出下列结论:①∠AME=108°;②五边形PFQNM∽五边形ABCDE;③AN2=AM•AD,其中正确的是( )