题目内容
7.在平面直角坐标系中,设点P到原点的距离为m,OP与x轴正方向的夹角为α,则[m,α]表示点P的极坐标,显然,点P的极坐标与它的坐标存在一一对应关系.例如:点P的坐标为($\sqrt{3}$,1),其极坐标为[2,30°],若点M的坐标为(2,2$\sqrt{3}$),则点M的极坐标为(4,60°).分析 根据极坐标的表示方法,可得答案.
解答 解:点M的坐标为(2,2$\sqrt{3}$),则点M的极坐标为长度为$\sqrt{{2}^{2}+(2\sqrt{3})^{2}}$=4,tanα=$\frac{2\sqrt{3}}{2}$=$\sqrt{3}$,α=60°,
点M的极坐标为(4,60°),
故答案为:(4,60°).
点评 本题考查了点的坐标,横坐标是点到原点的距离,角是与横轴标形成的角.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
2.中国首个空间实验室“天宫一号”于2011年9月29日21时16分发射升空,是中国人民实现全面载入航天飞行能力迈出意义非凡的一步,“天宫一号”由改进型“长征二号”火箭发射,火箭全长52米,起飞质量493000千克,其中数据“493000”用科学记数法表示为(保留两个有效数字)( )
| A. | 49.3×104 | B. | 4.93×105 | C. | 4.9×105 | D. | 4.9×106 |
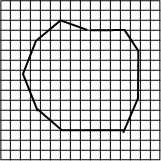 不规则面积的测量方法如下:把伞布放在方格纸上,在方格纸上描下它的轮廓,数一下图形中包含的方格数,对不满一格而大于半格的都算一格,小于半格的都舍去,总格数乘以每一格的面积,就是测量的总面积.在图中每小格的面积是1cm2,请估算不规则图形的面积约为100cm2.
不规则面积的测量方法如下:把伞布放在方格纸上,在方格纸上描下它的轮廓,数一下图形中包含的方格数,对不满一格而大于半格的都算一格,小于半格的都舍去,总格数乘以每一格的面积,就是测量的总面积.在图中每小格的面积是1cm2,请估算不规则图形的面积约为100cm2.