题目内容
7.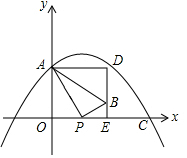 在如图所示的平面直角坐标系中,抛物线y=-$\frac{1}{6}$x2+bx+c过点A(0,4)和C(8,0),点P(t,0)是线段OC上的动点,PB⊥PA,且PB=$\frac{1}{2}$PA,过点B作x轴的垂线,过点A作y轴的垂线,两直线相交于点D;
在如图所示的平面直角坐标系中,抛物线y=-$\frac{1}{6}$x2+bx+c过点A(0,4)和C(8,0),点P(t,0)是线段OC上的动点,PB⊥PA,且PB=$\frac{1}{2}$PA,过点B作x轴的垂线,过点A作y轴的垂线,两直线相交于点D;(1)求抛物线的解析式;
(2)当t为何值时,点D落在抛物线上;
(3)是否存在t,使得以A,B,D为顶点的三角形与△AOP相似?若存在,求此时t的值;若不存在,请说明理由.
分析 (1)将A、C两点坐标代入抛物线y=-$\frac{1}{6}$x2+bx+c,运用待定系数法即可求出b,c的值;
(2)先求得M的坐标,进而求出点D的坐标,然后将D(t+2,4)代入(1)中求出的抛物线的解析式,即可求出t的值;
(3)由于t=8时,点B与点D重合,△ABD不存在,所以分0<t<8和t>8两种情况进行讨论,在每一种情况下,当以A、B、D为顶点的三角形与△PEB相似时,又分两种情况:△BEP∽△ADB与△PEB∽△ADB,根据相似三角形对应边的比相等列出比例式,求解即可.
解答 解:(1)∵抛物线y=-$\frac{1}{6}$x2+bx+c过点A(0,4)和C(8,0),
∴$\left\{\begin{array}{l}{c=4}\\{-\frac{1}{6}×64+8b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=\frac{5}{6}}\\{c=4}\end{array}\right.$.
故所求的抛物线解析式为:y=-$\frac{1}{6}$x2+$\frac{5}{6}$x+4;
(2)∵∠AOP=∠PEB=90°,∠OAP=∠EPB=90°-∠APO,
∴△AOP∽△PEB且相似比为$\frac{AO}{PE}$=$\frac{AP}{PB}$=2,
∵AO=4,
∴PE=2,OE=OP+PE=t+2,
又∵DE=OA=4,
∴点D的坐标为(t+2,4),
∴点D落在抛物线上时,有-$\frac{1}{6}$(t+2)2+$\frac{5}{6}$(t+2)+4=4,
解得t=3或t=-2,
∵t>0,
∴t=3.
故当t为3时,点D落在抛物线上;
(3)存在t,能够使得以A、B、D为顶点的三角形与△AOP相似,理由如下:
①当0<t<8时,如图1.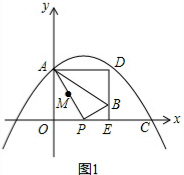
若△POA∽△ADB,则PO:AD=AO:BD,
即t:(t+2)=4:(4-$\frac{1}{2}$t),
整理,得t2+16=0,
∴t无解;
若△POA∽△BDA,同理,解得t=-2±2$\sqrt{5}$(负值舍去);
②当t>8时,如图2.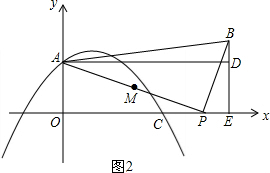
若△POA∽△ADB,则PO:AD=AO:BD,
即t:(t+2)=4:($\frac{1}{2}$t-4),
解得t=8±4$\sqrt{5}$(负值舍去);
若△POA∽△BDA,同理,解得t无解.
综上可知,当t=-2+2$\sqrt{5}$或8+4$\sqrt{5}$时,以A、B、D为顶点的三角形与△AOP相似.
点评 本题考查了待定系数法求函数的解析式,二次函数图象上点的坐标特征,旋转的性质,相似三角形的判定与性质,勾股定理等知识,综合性较强,难度较大.由相似三角形的判定与性质求出点D的坐标是解决(2)小题的关键;进行分类讨论是解决(3)小题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| 荔枝总质量n/Kg | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
| 损坏荔枝质量m/Kg | 5.50 | 10.50 | 15.15 | 19.42 | 24.25 | 30.93 | 35.32 | 39.24 | 44.57 | 51.51 |
| 荔枝损坏的频率$\frac{m}{n}$ | 0.110 | 0.105 | 0.101 | 0.097 | 0.097 | 0.103 | 0.101 | 0.098 | 0.099 | 0.103 |
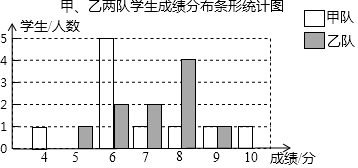
根据以上信息,请解答下面的问题:
(1)在下面甲、乙两队的成绩统计表中,a=6.8,b=7.5c=6.
| 平均分 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 | |
| 甲队 | a | 6 | c | 2.76 | 90% | 20% |
| 乙队 | 7.2 | b | 8 | 1.36 | 80% | 10% |
(3)甲队同学认为:甲队的合格率、优秀率均高于乙队,所以甲队的成绩好于乙队.但乙队同学不同意甲队同学的说法,认为乙队的成绩要好于甲队.请你写出两条支持乙队同学观点的理由.
(4)学校要从从甲、乙两队获得优秀的学生中,选取两名同学参加市级比赛,则恰好同时选中的两人均为甲队学生的概率为$\frac{1}{3}$.
| A. | 2 | B. | $\sqrt{5}$ | C. | 3 | D. | 4 |
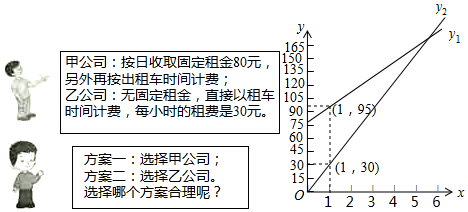 “五•一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
“五•一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游. 如图,点A、F、C、D在同一条直线上,已知AF=DC,∠A=∠D,BC∥EF,求证:AB=DE.
如图,点A、F、C、D在同一条直线上,已知AF=DC,∠A=∠D,BC∥EF,求证:AB=DE.