题目内容
16.已知菱形的周长为4$\sqrt{5}$,两条对角线的和为6,则菱形的面积为( )| A. | 2 | B. | $\sqrt{5}$ | C. | 3 | D. | 4 |
分析 由菱形的性质和勾股定理得出AO+BO=3,AO2+BO2=AB2,(AO+BO)2=9,求出2AO•BO=4,即可得出答案.
解答 解:如图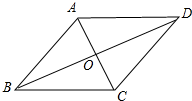 四边形ABCD是菱形,AC+BD=6,
四边形ABCD是菱形,AC+BD=6,
∴AB=$\sqrt{5}$,AC⊥BD,AO=$\frac{1}{2}$AC,BO=$\frac{1}{2}$BD,
∴AO+BO=3,
∴AO2+BO2=AB2,(AO+BO)2=9,
即AO2+BO2=5,AO2+2AO•BO+BO2=9,
∴2AO•BO=4,
∴菱形的面积=$\frac{1}{2}$AC•BD=2AO•BO=4;
故选:D.
点评 本题考查菱形的性质、勾股定理;解题的关键是记住菱形的面积公式,记住菱形的对角线互相垂直,属于中考常考题型.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
11. 如图由7个小正方体组合而成的几何体,它的主视图是( )
如图由7个小正方体组合而成的几何体,它的主视图是( )
 如图由7个小正方体组合而成的几何体,它的主视图是( )
如图由7个小正方体组合而成的几何体,它的主视图是( )| A. |  | B. |  | C. |  | D. |  |
8.下列成语描述的事件为随机事件的是( )
| A. | 水涨船高 | B. | 守株待兔 | C. | 水中捞月 | D. | 缘木求鱼 |
6.若△ABC~△DEF,相似比为3:2,则对应高的比为( )
| A. | 3:2 | B. | 3:5 | C. | 9:4 | D. | 4:9 |
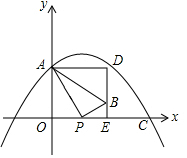 在如图所示的平面直角坐标系中,抛物线y=-$\frac{1}{6}$x2+bx+c过点A(0,4)和C(8,0),点P(t,0)是线段OC上的动点,PB⊥PA,且PB=$\frac{1}{2}$PA,过点B作x轴的垂线,过点A作y轴的垂线,两直线相交于点D;
在如图所示的平面直角坐标系中,抛物线y=-$\frac{1}{6}$x2+bx+c过点A(0,4)和C(8,0),点P(t,0)是线段OC上的动点,PB⊥PA,且PB=$\frac{1}{2}$PA,过点B作x轴的垂线,过点A作y轴的垂线,两直线相交于点D;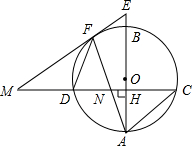 如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.
如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.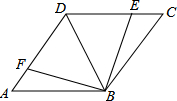 如图,点E,F分别在菱形ABCD的边DC,DA上,且CE=AF.
如图,点E,F分别在菱形ABCD的边DC,DA上,且CE=AF.