题目内容
2.先化简,再求值:$\frac{{x}^{2}+2x+1}{{x}^{2}-x}$÷(1+$\frac{2}{x-1}$),其中x=-2.分析 先根据分式的混合运算顺序和法则化简原式,再将x代入求值即可得.$\frac{{x}^{2}+2x+1}{{x}^{2}-x}$÷(1+$\frac{2}{x-1}$)
解答 解:原式=$\frac{(x+1)^{2}}{x(x-1)}$÷($\frac{x-1}{x-1}$+$\frac{2}{x-1}$)
=$\frac{(x+1)^{2}}{x(x-1)}$÷$\frac{x+1}{x-1}$
=$\frac{(x+1)^{2}}{x(x-1)}$•$\frac{x-1}{x+1}$
=$\frac{x+1}{x}$,
当x=-2时,原式=$\frac{-2+1}{-2}$=$\frac{1}{2}$.
点评 本题主要考查分式的化简求值,熟练掌握分式的混合运算顺序和法则是解题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
11. 如图由7个小正方体组合而成的几何体,它的主视图是( )
如图由7个小正方体组合而成的几何体,它的主视图是( )
 如图由7个小正方体组合而成的几何体,它的主视图是( )
如图由7个小正方体组合而成的几何体,它的主视图是( )| A. |  | B. |  | C. |  | D. |  |
12.下列曲线中不能表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
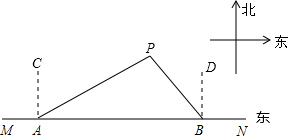 如图,船A、B在东西方向的海岸线MN上,均收到已搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,在船B的北偏西45°方向上,AB=30海里.
如图,船A、B在东西方向的海岸线MN上,均收到已搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,在船B的北偏西45°方向上,AB=30海里.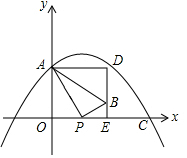 在如图所示的平面直角坐标系中,抛物线y=-$\frac{1}{6}$x2+bx+c过点A(0,4)和C(8,0),点P(t,0)是线段OC上的动点,PB⊥PA,且PB=$\frac{1}{2}$PA,过点B作x轴的垂线,过点A作y轴的垂线,两直线相交于点D;
在如图所示的平面直角坐标系中,抛物线y=-$\frac{1}{6}$x2+bx+c过点A(0,4)和C(8,0),点P(t,0)是线段OC上的动点,PB⊥PA,且PB=$\frac{1}{2}$PA,过点B作x轴的垂线,过点A作y轴的垂线,两直线相交于点D;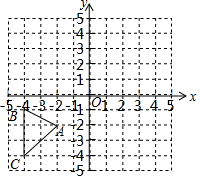 如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(-2,-2),B(-4,-1),C(-4,-4).
如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(-2,-2),B(-4,-1),C(-4,-4).