题目内容
19.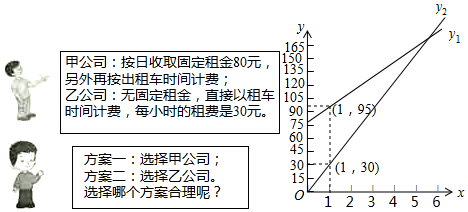 “五•一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
“五•一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.根据以上信息,解答下列问题:
(1)设租车时间为x小时,租用甲公司的车所需费用为y1元,租用乙公司的车所需费用为y2元,分别求出y1,y2关于x的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算.
分析 (1)根据函数图象中的信息,分别运用待定系数法,求得y1,y2关于x的函数表达式即可;
(2)当y1=y2时,15x+80=30x,当y1>y2时,15x+80>30x,当y1<y2时,15x+80>30x,分求得x的取值范围即可得出方案.
解答 解:(1)设y1=k1x+80,
把点(1,95)代入,可得
95=k1+80,
解得k1=15,
∴y1=15x+80(x≥0);
设y2=k2x,
把(1,30)代入,可得
30=k2,即k2=30,
∴y2=30x(x≥0);
(2)当y1=y2时,15x+80=30x,
解得x=$\frac{16}{3}$;
当y1>y2时,15x+80>30x,
解得x<$\frac{16}{3}$;
当y1<y2时,15x+80<30x,
解得x>$\frac{16}{3}$;
∴当租车时间为$\frac{16}{3}$小时,选择甲乙公司一样合算;当租车时间小于$\frac{16}{3}$小时,选择乙公司合算;当租车时间大于$\frac{16}{3}$小时,选择甲公司合算.
点评 本题主要考查了一次函数的应用,解题时注意:求正比例函数y=kx,只要一对x,y的值;而求一次函数y=kx+b,则需要两组x,y的值.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
11. 如图由7个小正方体组合而成的几何体,它的主视图是( )
如图由7个小正方体组合而成的几何体,它的主视图是( )
 如图由7个小正方体组合而成的几何体,它的主视图是( )
如图由7个小正方体组合而成的几何体,它的主视图是( )| A. |  | B. |  | C. |  | D. |  |
8.下列成语描述的事件为随机事件的是( )
| A. | 水涨船高 | B. | 守株待兔 | C. | 水中捞月 | D. | 缘木求鱼 |
9.计算(a2)3+a2•a3-a2÷a-3,结果是( )
| A. | 2a5-a | B. | 2a5-$\frac{1}{a}$ | C. | a5 | D. | a6 |
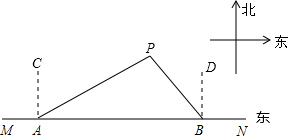 如图,船A、B在东西方向的海岸线MN上,均收到已搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,在船B的北偏西45°方向上,AB=30海里.
如图,船A、B在东西方向的海岸线MN上,均收到已搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,在船B的北偏西45°方向上,AB=30海里.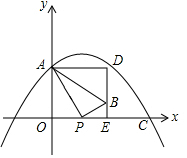 在如图所示的平面直角坐标系中,抛物线y=-$\frac{1}{6}$x2+bx+c过点A(0,4)和C(8,0),点P(t,0)是线段OC上的动点,PB⊥PA,且PB=$\frac{1}{2}$PA,过点B作x轴的垂线,过点A作y轴的垂线,两直线相交于点D;
在如图所示的平面直角坐标系中,抛物线y=-$\frac{1}{6}$x2+bx+c过点A(0,4)和C(8,0),点P(t,0)是线段OC上的动点,PB⊥PA,且PB=$\frac{1}{2}$PA,过点B作x轴的垂线,过点A作y轴的垂线,两直线相交于点D;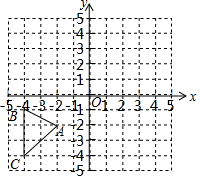 如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(-2,-2),B(-4,-1),C(-4,-4).
如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(-2,-2),B(-4,-1),C(-4,-4).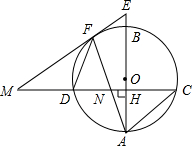 如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.
如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.