题目内容

17．已知a，b，c为△ABC的三边，且满足a2+b2+c2+50=6a+8b+10c．求证：这个三角形是直角三角形．

分析 已知等式变形后，利用非负数的性质求出a，b及c的值，即可对于三角形形状进行判断．

解答 证明：∵a2+b2+c2+50=6a+8b+10c，
∴（a-3）2+（b-4）2+（c-5）2=0，
∴a=3，b=4，c=5，
∵32+42=52，
∴三角形为直角三角形．

点评 此题考查了因式分解的应用，以及非负数的性质，熟练掌握完全平方公式是解本题的关键．

练习册系列答案
相关题目
7．如图，在△ABC中，AB=AC，BD⊥AC于D，CE⊥AB于E，BD、CE相交于F．求证：∠BCE=∠CBD．
8．若y=$\sqrt{4x-3}$+$\sqrt{3-4x}$-5，则x=$\frac{3}{4}$，y=-5．
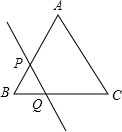5．如图，在正△ABC中，AB=10cm，直线PQ由点B出发，沿BA的方向匀速运动，速度为1cm/s，运动时间为t（s）（0＜t＜5），则BP=$\frac{2\sqrt{3}}{3}t$．（用t的代数式表示）
12．若方程①x2+x-1=0的两根分别为x1，x2，则x1+x2=-1，x1x2=-1；反过来，若x1+x2=-1，x1x2=-1，则相应的一元二次方程为x2+x-1=0；②3x2-4x-7=0的两根为x1，x2．则x1+x2=$\frac{4}{3}$，x1x2=$\frac{7}{3}$；反过来，若x1+x2=$\frac{4}{3}$，x1x2=$\frac{7}{3}$，则相应的一元二次方程为3x2-4x-7=0．
问题：
（1）若方程的两根为x1=p，x2=q，则相应的一元二次方程为x2-px+q=0；
（2）若方程的两根为x1，x2，且x1+x2=$\frac{b}{a}$，x1x2=$\frac{c}{a}$，则相应的一元二次方程可以为ax2-bx+c=0
（3）已知方程x2+mx-n=0（n≠0），求一个一元二次方程，使它的根分别是已知方程两根的倒数．
2．若长方形的一边长为3m+n，另一边比它长m-n（m＞n），则这个长方形的面积是（　　）
A．12m2+4mnB．12m2-4mnC．3m2-2mn-n2D．3m2+2mn-n2
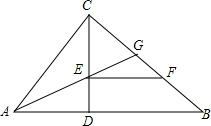9．如图，△ABC中，∠ACB=90°，CD是高，AG平分∠CAB，EF∥AB，AC=6，BC=8．
（1）求证：CE=FB；
（2）求FG的长．
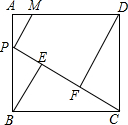13．如图，P为正方形ABCD的边AB上的一个动点（点P不与A、B重合），连结PC，作BE⊥PC，DF⊥PC，垂足分别为点E、F，已知AD=5．
（1）求BE2+DF2的值；
（2）过点P作PM∥DF交AD于点M，问：点P在何位置时线段AM最长，并求出此时AM的值．
14．（1）若（m-2）2+|n+3|=0，求3m-n2的值．
（2）a、b在数轴上的位置如图所示，化简：|a+b|-2|b-a|=b-3a．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网