题目内容
7.在图1至图3中,△ABC是等边三角形,点E在AB上,点D在CB的延长线上,且ED=EC.
观察思考:
(1)当点E为AB的中点时,如图1,线段AE与DB的大小关系是:AE=DB(填“>”,“<”或“=”);
拓展延伸:
(2)当点E不是AB的中点时,如图2,猜想线段AE与DB的大小关系是:AE=DB(填“>”,“<”或“=”),并说明理由(提示:在图2中,过点E作EF∥BC交AC于点F,得到图3).
分析 (1)由等边三角形的性质得出AE=BE,∠BCE=30°,再由DE=EC即可得出∠EDC=∠BCE=30°,进而得出BD=BE即可得出结论;
(2)先判断出BE=CF,再判断出∠BED=∠FCE,即可得出△DBE≌△EFC,结论得证.
解答 解:(1)∵点E是等边三角形ABC的边AB的中点,
∴AE=BE,∠ABC=60°,∠BCE=30°,
∵DE=EC,
∴∠EDC=∠BCE=30°,
∵∠ABC=60°,
∴∠BED=30°=∠CDE,
∴BD=BE,
∵AE=BE,
∴AE=BD;
故答案为:=
(2)=;
理由:过点E作EF∥BC交AC于点F,
在等边△ABC中,∠ABC=∠ACB=∠BAC=60°,AB=BC=AC,
∵EF∥BC,
∴∠AEF=∠AFE=60°=∠BAC,
∴AE=AF=EF,
∴AB-AE=AC-AF,
即BE=CF,
∵ED=EC,
∴∠EDB=∠ECB,
∵∠ABC=∠EDB+∠BED=60°,
∠ACB=∠ECB+∠FCE=60°,
∴∠BED=∠FCE,
∴△DBE≌△EFC,
∴DB=EF,
∴AE=DB.
故答案为:=.
点评 此题是三角形综合题,主要考查了等边三角形的性质,全等三角形的判定和性质,作出辅助线是解本题的关键.

练习册系列答案
相关题目
12.已知某种型号的纸100张的厚度约为1cm,那么这种型号的纸13亿张的厚度约为( )
| A. | 1.3×105km | B. | 1.3×104km | C. | 1.3×103km | D. | 1.3×102km |
19.一次函数y=kx+b(k≠0)中变量x与y的部分对应值如表
下列结论:
①y随x的增大而减小;
②x=2是方程(k-1)x+b=0的解;
③当x<2时,(k-1)x+b<0.
其中正确的个数为( )
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 8 | 6 | 4 | 2 | 0 | … |
①y随x的增大而减小;
②x=2是方程(k-1)x+b=0的解;
③当x<2时,(k-1)x+b<0.
其中正确的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
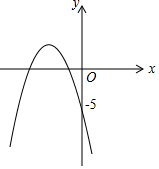 已知抛物线y=ax2+x+b上的一点为(-1,-7),与y轴交点为(0,-5)
已知抛物线y=ax2+x+b上的一点为(-1,-7),与y轴交点为(0,-5)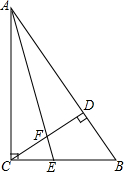 已知:如图,在△ABC中,∠ACB=90°,AE是∠BAC的角平分线,CD是高,AE与CD相交于点F.
已知:如图,在△ABC中,∠ACB=90°,AE是∠BAC的角平分线,CD是高,AE与CD相交于点F.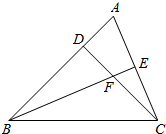 如图,D是AB上的一点,E是AC上的一点,BE、CD相交于一点F,∠A=63°,∠ACD=34°,∠ABE=20°,求∠BDC和∠BFC的度数.
如图,D是AB上的一点,E是AC上的一点,BE、CD相交于一点F,∠A=63°,∠ACD=34°,∠ABE=20°,求∠BDC和∠BFC的度数. 如图,已知AB=AC,AD平分∠BAC,试说明∠EBD=∠ECD.
如图,已知AB=AC,AD平分∠BAC,试说明∠EBD=∠ECD.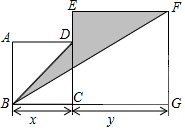 如图:四边形ABCD和四边形ECGF都是正方形,其边长分别为x、y(点B、C、G和点C、D、E分别在一条直线上)则图中阴影部分的面积为:$\frac{1}{2}{x}^{2}-\frac{1}{2}xy+\frac{1}{2}{y}^{2}$(用含x、y的代数式表示,且按x降幂排列)
如图:四边形ABCD和四边形ECGF都是正方形,其边长分别为x、y(点B、C、G和点C、D、E分别在一条直线上)则图中阴影部分的面积为:$\frac{1}{2}{x}^{2}-\frac{1}{2}xy+\frac{1}{2}{y}^{2}$(用含x、y的代数式表示,且按x降幂排列)