题目内容
20.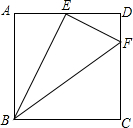 如图,在正方形ABCD中,边长为4,点E、F分别在边AD和CD上,其中AE=2,DF=1,判断BE与EF的位置关系并说明理由.
如图,在正方形ABCD中,边长为4,点E、F分别在边AD和CD上,其中AE=2,DF=1,判断BE与EF的位置关系并说明理由.
分析 根据正方形的性质及条件求出ED、CF的值,再由勾股定理就可以求出BF、BE及EF的值,再根据勾股定理的逆定理就可以直接求出△BEF是直角三角形,从而可以得出结论.
解答 解:BE⊥EF.
理由:∵正方形ABCD中,边长为4,AE=2,DF=1,
∴ED=2,CF=3,AB=BC=4,
在Rt△ABE中,
BE=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
在Rt△BCF中
BF=$\sqrt{{4}^{2}+{3}^{2}}$=5
在Rt△EDF中
EF=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
在△BEF中,BE2+EF2=(2$\sqrt{5}$)2+($\sqrt{5}$)2=25=BF2,
∴△BEF是直角三角形,且∠BEF=90°,
∴BE⊥EF.
点评 本题考查了正方形的性质的运用,勾股定理的运用及勾股定理的逆定理的运用.在解答中求出△BEF的三边长的是关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
10.在一次实验中,测得两个变量x与y之间的对应值如下表所示:
(1)根据表中数据,请探究y与x之间的函数关系式;
(2)根据你的关系式,求出当y=-15时x的值;
(3)当x从-10连续变化到15时,指出y的变化规律并求出y的最大值和最小值?
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | -5 | -3 | -1 | 1 | 3 | 5 | 7 | … |
(2)根据你的关系式,求出当y=-15时x的值;
(3)当x从-10连续变化到15时,指出y的变化规律并求出y的最大值和最小值?
11. 如图,∠AOC=∠BOD=90°,∠AOD=140°,则∠BOC的度数为( )
如图,∠AOC=∠BOD=90°,∠AOD=140°,则∠BOC的度数为( )
 如图,∠AOC=∠BOD=90°,∠AOD=140°,则∠BOC的度数为( )
如图,∠AOC=∠BOD=90°,∠AOD=140°,则∠BOC的度数为( )| A. | 30° | B. | 45° | C. | 50° | D. | 40° |
8. 如图,在△ABC中,DE∥BC,∠A=60°,∠ADE=50°,则∠C的度数为( )
如图,在△ABC中,DE∥BC,∠A=60°,∠ADE=50°,则∠C的度数为( )
 如图,在△ABC中,DE∥BC,∠A=60°,∠ADE=50°,则∠C的度数为( )
如图,在△ABC中,DE∥BC,∠A=60°,∠ADE=50°,则∠C的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
5.关于x的一元二次方程ax2+bx+c=0(a≠0,b2-4ac>0)的根是( )
| A. | $\frac{b±\sqrt{b^2-4ac}}{2a}$ | B. | $\frac{-b+\sqrt{b^2-4ac}}{2a}$ | C. | $\frac{-b±\sqrt{b^2-4ac}}{2}$ | D. | $\frac{-b±\sqrt{b^2-4ac}}{2a}$ |
 如图,在△ABC中,D为三角形内一点,∠A=35°,∠ABD=20°,∠ACD=25°,BD∥CE,则∠DCE=75°.
如图,在△ABC中,D为三角形内一点,∠A=35°,∠ABD=20°,∠ACD=25°,BD∥CE,则∠DCE=75°.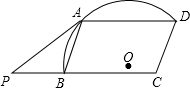 如图,在?ABCD中,∠ABC=70°,半径为r的⊙O经过点A,B,D,$\widehat{AD}$的长是$\frac{πr}{2}$,延长CB至点P,使得PB=AB.判断直线PA与⊙O的位置关系,并说明理由.
如图,在?ABCD中,∠ABC=70°,半径为r的⊙O经过点A,B,D,$\widehat{AD}$的长是$\frac{πr}{2}$,延长CB至点P,使得PB=AB.判断直线PA与⊙O的位置关系,并说明理由.