题目内容
17．
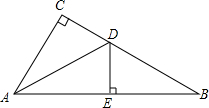如图，在Rt△ABC中，∠C=90°，DE垂直平分AB分别交BC、AB于点D、E，且CD=DE，求∠B的度数．
分析 根据线段垂直平分线的性质得到DA=DB，根据等边对等角得到∠DAB=∠B，根据角平分线的判定定理得到∠CAD=∠DAB，计算即可．
解答 解：∵DE垂直平分AB，
∴DA=DB，
∴∠DAB=∠B，
∵∠C=90°，DE⊥AB，CD=DE，
∴∠CAD=∠DAB，
∴∠DAB=∠B=∠CAD，
∴∠B=30°．
点评 本题考查的是角平分线的判定和线段垂直平分线的性质，掌握角平分线的判定定理和垂直平分线上的点，到线段两端点的距离相等是解题的关键．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
8．
如图，在△ABC中，DE∥BC，∠A=60°，∠ADE=50°，则∠C的度数为（ ）
如图，在△ABC中，DE∥BC，∠A=60°，∠ADE=50°，则∠C的度数为（ ）| A． | 50° | B． | 60° | C． | 70° | D． | 80° |
5．关于x的一元二次方程ax2+bx+c=0（a≠0，b2-4ac＞0）的根是（ ）
| A． | $\frac{b±\sqrt{b^2-4ac}}{2a}$ | B． | $\frac{-b+\sqrt{b^2-4ac}}{2a}$ | C． | $\frac{-b±\sqrt{b^2-4ac}}{2}$ | D． | $\frac{-b±\sqrt{b^2-4ac}}{2a}$ |
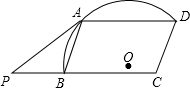如图，在?ABCD中，∠ABC=70°，半径为r的⊙O经过点A，B，D，$\widehat{AD}$的长是$\frac{πr}{2}$，延长CB至点P，使得PB=AB．判断直线PA与⊙O的位置关系，并说明理由．
2．数轴上与原点距离为5的点表示的是（ ）
| A． | 5 | B． | -5 | C． | ±5 | D． | 6 |
7．下列说法错误的是（ ）
| A． | π是有理数 | B． | 两点之间线段最短 | ||
| C． | x2-x是二次二项式 | D． | 正数的绝对值是它本身 |