题目内容
7.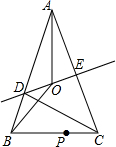 如图,在△ABC中,AB=AC,AC的垂直平分线交AB于D,交AC于E,AO平分∠BAC交DE于O.
如图,在△ABC中,AB=AC,AC的垂直平分线交AB于D,交AC于E,AO平分∠BAC交DE于O.(1)若AC=27,△BCD周长等于50,求BC的长;
(2)若∠BAC=40°,在BC上存在一点P(P不与B、C重合),使得△BOP是等腰三角形,求∠BPO的度数.
分析 (1)利用线段垂直平分线得的性质得DA=DC,再利用等线段代换和三角形周长定理得到BC+AC=50,所以BC=50-AC=23;
(2)连接OC,如图,根据等腰三角形的性质得AO垂直平分BC,根据三角形内角和可就是出∠ABC=∠ACB=70°,再证明OA=OC得到∠1=∠2=20°,则∠OBC=∠OCB=50°,然后讨论:当BO=BP时,根据等腰三角形的性质和三角形内角和得到∠BPO=65°;当PO=PB时,同样方法得到∠BPO=80°.
解答 解:(1)∵AC的垂直平分线交AB于D,
∴DA=DC,
∵△BCD周长等于50,
即BC+BD+CD=50,
∴BC+BD+AD=50,
即BC+AC=50,
∴BC=50-27=23;
(2)连接OC,如图,
∵AB=AC,AO平分∠BAC,
∴AO垂直平分BC,∠1=20°,∠ABC=∠ACB=$\frac{1}{2}$(180°-∠BAC)=70°,
∴OB=OC,
∵OE垂直平分AC,
∴OA=OC,
∴∠1=∠2=20°,
∴∠BCO=70°-20°=50°,
∴∠OBC=∠OCB=50°,
当BO=BP时,∠BPO=$\frac{1}{2}$(180°-50°)=65°;
当PO=PB时,∠BPO=180°-2×50°=80°,
综上所述,∠BPO的度数为65°或80°.
点评 本题考查了线段垂直平分线的性质:垂直平分线垂直且平分其所在线段;垂直平分线上任意一点,到线段两端点的距离相等;三角形三条边的垂直平分线相交于一点,该点叫外心,并且这一点到三个顶点的距离相等.

练习册系列答案
相关题目
 如图,在△ABC中,AB=AC,AB的垂直平分线DG交AC于点G,若AD+AC=24cm,BD+BC=20cm,求△BGC的周长.
如图,在△ABC中,AB=AC,AB的垂直平分线DG交AC于点G,若AD+AC=24cm,BD+BC=20cm,求△BGC的周长.



 ?ABCD中,有一点P,使∠APD=∠ADP.连接AP、BP、DP、CP,求证:∠PAD=∠PCB.
?ABCD中,有一点P,使∠APD=∠ADP.连接AP、BP、DP、CP,求证:∠PAD=∠PCB.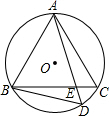 如图,△ABC是⊙O的内接等边三角形,D为⊙O上的一点,AD与BC交于点E,AE=4cm,DE=1cm,求AB的长.
如图,△ABC是⊙O的内接等边三角形,D为⊙O上的一点,AD与BC交于点E,AE=4cm,DE=1cm,求AB的长.