题目内容
16.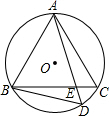 如图,△ABC是⊙O的内接等边三角形,D为⊙O上的一点,AD与BC交于点E,AE=4cm,DE=1cm,求AB的长.
如图,△ABC是⊙O的内接等边三角形,D为⊙O上的一点,AD与BC交于点E,AE=4cm,DE=1cm,求AB的长.
分析 根据等边三角形的性质和圆周角定理证出△BAE∽△DAB,根据相似三角形的性质列出比例式计算即可.
解答 解:∵△ABC是等边三角形,
∴∠ABC=∠C=60°,
∴∠D=∠C=60°;
∴∠ABC=∠D,又∠BAE=∠DAB,
∴△BAE∽△DAB,
∴AB2=AE•AD=4×(4+1)=20,
∴AB=2$\sqrt{5}$cm.
点评 本题考查的是等边三角形的性质、圆周角定理和相似三角形的判定和性质定理;熟练掌握等边三角形的性质和圆周角定理,证明三角形相似得出比例式是解决问题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
1.分式$\frac{x}{x-1}$+$\frac{1}{1-x}$可化简为( )
| A. | $\frac{x+1}{x-1}$ | B. | 1 | C. | -1 | D. | $\frac{x+1}{1-x}$ |
6.下列结论中,不正确的是( )
| A. | 两点确定一条直线 | |
| B. | 等角的余角相等 | |
| C. | 过一点有且只有一条直线与已知直线平行 | |
| D. | 对顶角相等 |
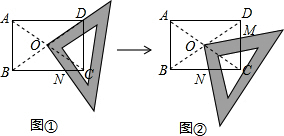
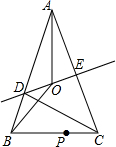 如图,在△ABC中,AB=AC,AC的垂直平分线交AB于D,交AC于E,AO平分∠BAC交DE于O.
如图,在△ABC中,AB=AC,AC的垂直平分线交AB于D,交AC于E,AO平分∠BAC交DE于O.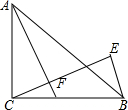 如图,△ABC中,∠ACB=90°,AC=BC,D为BC的中点,CF⊥AD于F,BE⊥CF交CF的延长线于E,求$\frac{BE}{AF}$的值.
如图,△ABC中,∠ACB=90°,AC=BC,D为BC的中点,CF⊥AD于F,BE⊥CF交CF的延长线于E,求$\frac{BE}{AF}$的值.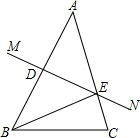 如图,在△ABC中,AB的垂直平分线MN交AB于点D,交AC于点E,且AC=15cm,△BCE的周长等于25cm.
如图,在△ABC中,AB的垂直平分线MN交AB于点D,交AC于点E,且AC=15cm,△BCE的周长等于25cm.