题目内容
18.如果1<x<2,试化简$\frac{|x-2|}{2-x}$-$\frac{x-1}{|x-1|}$+$\frac{|x|}{x}$.分析 根据1<x<2,可以将所求的式子中的绝对值去掉,从而可以对所求的式子进行化简,本题得以解决.
解答 解:∵1<x<2,
∴x-2<0,x-1>0,
∴$\frac{|x-2|}{2-x}$-$\frac{x-1}{|x-1|}$+$\frac{|x|}{x}$
=$\frac{2-x}{2-x}-\frac{x-1}{x-1}+\frac{x}{x}$
=1-1+1
=1.
点评 本题考查分式的加减法、解题的关键是明确分式加减法的计算方法,会根据x的取值范围,将绝对值的符号去掉.

练习册系列答案
相关题目
11.一个不透明的盒子中装有6个大小相同的乒乓球,其中4个是黄球,2个是白球.从该盒子中任意摸出一个球,摸到黄球的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{5}$ |
3.若整数x能使分式$\frac{3x-3}{{x}^{2}-1}$的值是整数,则符合条件的x的值有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
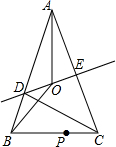 如图,在△ABC中,AB=AC,AC的垂直平分线交AB于D,交AC于E,AO平分∠BAC交DE于O.
如图,在△ABC中,AB=AC,AC的垂直平分线交AB于D,交AC于E,AO平分∠BAC交DE于O.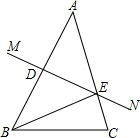 如图,在△ABC中,AB的垂直平分线MN交AB于点D,交AC于点E,且AC=15cm,△BCE的周长等于25cm.
如图,在△ABC中,AB的垂直平分线MN交AB于点D,交AC于点E,且AC=15cm,△BCE的周长等于25cm.