题目内容
15．化简：（$\frac{2x-3}{x}$-1）÷$\frac{{x}^{2}-9}{{x}^{2}+3x}$．分析 首先将括号里面通分运算，进而分解因式化简求出答案．
解答 解：（$\frac{2x-3}{x}$-1）÷$\frac{{x}^{2}-9}{{x}^{2}+3x}$
=$\frac{2x-3-x}{x}$×$\frac{x（x+3）}{（x+3）（x-3）}$
=$\frac{x-3}{x}$•$\frac{x}{x-3}$
=1．
点评 此题主要考查了分式的混合运算，正确分解因式是解题关键．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
8．
如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O1，O2，O3，…组成一条平滑的曲线．点P从原点O出发，沿这条曲线向右运动，速度为每秒$\frac{π}{2}$个单位长度，则第15秒时，点P的坐标是（ ）
如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O1，O2，O3，…组成一条平滑的曲线．点P从原点O出发，沿这条曲线向右运动，速度为每秒$\frac{π}{2}$个单位长度，则第15秒时，点P的坐标是（ ）| A． | （15，1） | B． | （15，-1） | C． | （30，1） | D． | （30，-1） |
3．若整数x能使分式$\frac{3x-3}{{x}^{2}-1}$的值是整数，则符合条件的x的值有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
20．
如图，直线y=$\frac{1}{2}$x+2交x轴于A点，将一块等腰直角三角形纸板的直角顶点置于原点O，另两个顶点M、N恰好落在直线y=$\frac{1}{2}$x+2上．则S△M0N=（ ）
如图，直线y=$\frac{1}{2}$x+2交x轴于A点，将一块等腰直角三角形纸板的直角顶点置于原点O，另两个顶点M、N恰好落在直线y=$\frac{1}{2}$x+2上．则S△M0N=（ ）| A． | $\frac{12}{5}$ | B． | $\frac{14}{5}$ | C． | $\frac{16}{5}$ | D． | 4 |
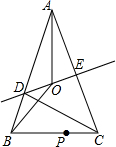如图，在△ABC中，AB=AC，AC的垂直平分线交AB于D，交AC于E，AO平分∠BAC交DE于O．
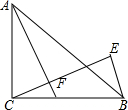如图，△ABC中，∠ACB=90°，AC=BC，D为BC的中点，CF⊥AD于F，BE⊥CF交CF的延长线于E，求$\frac{BE}{AF}$的值．