题目内容
11.若关于x的方程x+$\frac{2}{x}$=c+$\frac{2}{c}$的根为x1=c,x2=$\frac{2}{c}$,则关于x的方程x+$\frac{2}{x-1}$=a+$\frac{2}{a-1}$的根是( )| A. | x1=a,x2=$\frac{2}{a-1}$ | B. | x1=a-1,x2=$\frac{2}{a-1}$ | C. | x1=a,x2=$\frac{a+1}{a-1}$ | D. | x1=a,x2=$\frac{a}{a-1}$ |
分析 由方程x+$\frac{2}{x-1}$=a+$\frac{2}{a-1}$得:x-1+$\frac{2}{x-1}$=a-1+$\frac{2}{a-1}$,把x-1看作一个整体,再根据题目信息解答即可求解.
解答 解:由方程x+$\frac{2}{x-1}$=a+$\frac{2}{a-1}$得:x-1+$\frac{2}{x-1}$=a-1+$\frac{2}{a-1}$,
根据题意,知:x-1=a-1或x-1=$\frac{2}{a-1}$,
解得:x1=a,x2=$\frac{a+1}{a-1}$,
故选:C.
点评 本题考查了分式方程的解,读懂题目提供的信息是求解的根本,将待求解方程变形成符合规律的方程是解题的关键,注意整体思想的应用.

练习册系列答案
相关题目
19.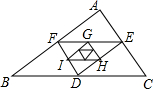 如图,△DEF的顶点分别是△ABC各边的中点,△GHI的顶点分别是△DEF各边的中点,…,依次做下去,记△ABC得周长为P1,△DEF的周长为P2,△GHI的周长为P3,…,已知P1=1,则Pn等于( )
如图,△DEF的顶点分别是△ABC各边的中点,△GHI的顶点分别是△DEF各边的中点,…,依次做下去,记△ABC得周长为P1,△DEF的周长为P2,△GHI的周长为P3,…,已知P1=1,则Pn等于( )
 如图,△DEF的顶点分别是△ABC各边的中点,△GHI的顶点分别是△DEF各边的中点,…,依次做下去,记△ABC得周长为P1,△DEF的周长为P2,△GHI的周长为P3,…,已知P1=1,则Pn等于( )
如图,△DEF的顶点分别是△ABC各边的中点,△GHI的顶点分别是△DEF各边的中点,…,依次做下去,记△ABC得周长为P1,△DEF的周长为P2,△GHI的周长为P3,…,已知P1=1,则Pn等于( )| A. | $\frac{1}{{2}^{n-1}}$ | B. | $\frac{1}{{2}^{n}}$ | C. | $\frac{1}{{2}^{n+1}}$ | D. | $\frac{1}{{2}^{n+2}}$ |
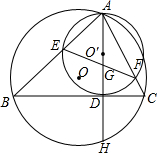 如图,延长△ABC的高AD和它的外接圆交于H,AD为直径作圆交AB、AC于E、F两点,EF交AD于G.求证:AD2=AG•AH.
如图,延长△ABC的高AD和它的外接圆交于H,AD为直径作圆交AB、AC于E、F两点,EF交AD于G.求证:AD2=AG•AH.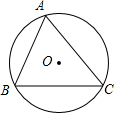 如图,⊙O是△ABC的外接圆,⊙O的半径是R=2,sinA=0.8,则弦BC的长为3.2.
如图,⊙O是△ABC的外接圆,⊙O的半径是R=2,sinA=0.8,则弦BC的长为3.2.