题目内容
6.宜宾市某化工厂,现有A种原料52千克,B种原料64千克,现用这些原料生产甲、乙两种产品共20件.已知生产1件甲种产品需要A种原料3千克,B种原料2千克;生产1件乙种产品需要A种原料2千克,B种原料4千克,则生产方案的种数为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 设生产甲产品x件,则乙产品(20-x)件,根据生产1件甲种产品需要A种原料3千克,B种原料2千克;生产1件乙种产品需要A种原料2千克,B种原料4千克,列出不等式组,求出不等式组的解,再根据x为整数,得出有5种生产方案.
解答 解:设生产甲产品x件,则乙产品(20-x)件,根据题意得:
$\left\{\begin{array}{l}{3x+2(20-x)≤52}\\{2x+4(20-x)≤64}\end{array}\right.$,
解得:8≤x≤12,
∵x为整数,
∴x=8,9,10,11,12,
∴有5种生产方案:
方案1,A产品8件,B产品12件;
方案2,A产品9件,B产品11件;
方案3,A产品10件,B产品10件;
方案4,A产品11件,B产品9件;
方案5,A产品12件,B产品8件;
故选B.
点评 此题考查了一元一次不等式组的应用,解决问题的关键是读懂题意,找到关键描述语,找到所求的量的数量关系,列出不等式组.

练习册系列答案
相关题目
1. 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )| A. | 4 | B. | 4$\sqrt{2}$ | C. | 6 | D. | 4$\sqrt{3}$ |

 某学校在“你最喜欢的球类运动”调查中.随机调查了若干名学生(每名学生只能选取一项球类运动),并根据调查结果绘制了如图所示的扇形统计图.已知其中最喜欢羽毛球的人数比最喜欢乒乓球的人数少6人.则该校被调査的学生总人数为60人.
某学校在“你最喜欢的球类运动”调查中.随机调查了若干名学生(每名学生只能选取一项球类运动),并根据调查结果绘制了如图所示的扇形统计图.已知其中最喜欢羽毛球的人数比最喜欢乒乓球的人数少6人.则该校被调査的学生总人数为60人.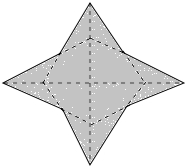 如图,把一个菱形绕着它的对角线的交点旋转90°,旋转前后的两个菱形构成一个“星形”(阴影部分),若菱形的一个内角为60°,边长为2,则该“星形”的面积是6$\sqrt{3}$-6.
如图,把一个菱形绕着它的对角线的交点旋转90°,旋转前后的两个菱形构成一个“星形”(阴影部分),若菱形的一个内角为60°,边长为2,则该“星形”的面积是6$\sqrt{3}$-6.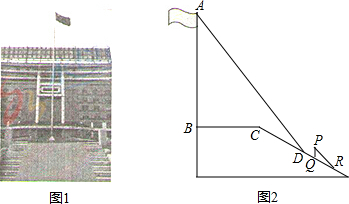
 如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=$3\sqrt{2}$,CD=$2\sqrt{2}$,点P是四边形ABCD四条边上的一个动点,若P到BD的距离为$\frac{5}{2}$,则满足条件的点P有2个.
如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=$3\sqrt{2}$,CD=$2\sqrt{2}$,点P是四边形ABCD四条边上的一个动点,若P到BD的距离为$\frac{5}{2}$,则满足条件的点P有2个. 如图,已知直线l1∥l2,将等边三角形如图放置,若∠α=40°,则∠β等于20°.
如图,已知直线l1∥l2,将等边三角形如图放置,若∠α=40°,则∠β等于20°.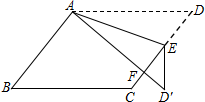 如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为36°.
如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为36°.