题目内容
1. 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )| A. | 4 | B. | 4$\sqrt{2}$ | C. | 6 | D. | 4$\sqrt{3}$ |
分析 根据AD是中线,得出CD=4,再根据AA证出△CBA∽△CAD,得出$\frac{AC}{BC}$=$\frac{CD}{AC}$,求出AC即可.
解答 解:∵BC=8,
∴CD=4,
在△CBA和△CAD中,
∵∠B=∠DAC,∠C=∠C,
∴△CBA∽△CAD,
∴$\frac{AC}{BC}$=$\frac{CD}{AC}$,
∴AC2=CD•BC=4×8=32,
∴AC=4$\sqrt{2}$;
故选B.
点评 此题考查了相似三角形的判断与性质,关键是根据AA证出△CBA∽△CAD,是一道基础题.

练习册系列答案
相关题目
9.关于一组数据:2,4,8,3,3,下列说法不正确的是( )
| A. | 中位数是3 | B. | 众数是3 | C. | 平均数是4 | D. | 方差是4 |
10.一次函数y=$\frac{4}{3}$x-b与y=$\frac{4}{3}$x-1的图象之间的距离等于3,则b的值为( )
| A. | -2或4 | B. | 2或-4 | C. | 4或-6 | D. | -4或6 |
11.已知点A(a,1)与点A′(5,b)关于坐标原点对称,则实数a、b的值是( )
| A. | a=5,b=1 | B. | a=-5,b=1 | C. | a=5,b=-1 | D. | a=-5,b=-1 |
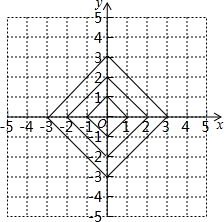 在平面直角坐标系中,横坐标,纵坐标都为整数的点称为整点,正方形边长的整点称为边整点,如图,第一个正方形有4个边整点,第二个正方形有8个边整点,第三个正方形有12个边整点,…,按此规律继续作下去,若从内向外共作了5个这样的正方形,那么其边整点的个数共有60个,这些边整点落在函数y=$\frac{4}{x}$的图象上的概率是$\frac{1}{10}$.
在平面直角坐标系中,横坐标,纵坐标都为整数的点称为整点,正方形边长的整点称为边整点,如图,第一个正方形有4个边整点,第二个正方形有8个边整点,第三个正方形有12个边整点,…,按此规律继续作下去,若从内向外共作了5个这样的正方形,那么其边整点的个数共有60个,这些边整点落在函数y=$\frac{4}{x}$的图象上的概率是$\frac{1}{10}$.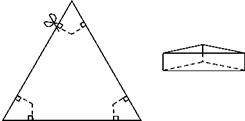 如图,以边长为20cm的正三角形纸板的各顶点为端点,在各边上分别截取4cm长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形.把它们沿图中 虛线剪掉,用剩下的纸板折成一个底为正三角形的无盖柱形盒子,则它的容积为144cm3.
如图,以边长为20cm的正三角形纸板的各顶点为端点,在各边上分别截取4cm长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形.把它们沿图中 虛线剪掉,用剩下的纸板折成一个底为正三角形的无盖柱形盒子,则它的容积为144cm3.