题目内容
18. 如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=$3\sqrt{2}$,CD=$2\sqrt{2}$,点P是四边形ABCD四条边上的一个动点,若P到BD的距离为$\frac{5}{2}$,则满足条件的点P有2个.
如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=$3\sqrt{2}$,CD=$2\sqrt{2}$,点P是四边形ABCD四条边上的一个动点,若P到BD的距离为$\frac{5}{2}$,则满足条件的点P有2个.
分析 首先作出AB、AD边上的点P(点A)到BD的垂线段AE,即点P到BD的最长距离,作出BC、CD的点P(点C)到BD的垂线段CF,即点P到BD的最长距离,由已知计算出AE、CF的长为$\frac{5}{2}$,比较得出答案.
解答  解:过点A作AE⊥BD于E,过点C作CF⊥BD于F,
解:过点A作AE⊥BD于E,过点C作CF⊥BD于F,
∵∠BAD=∠ADC=90°,AB=AD=$3\sqrt{2}$,CD=2$\sqrt{2}$,
∴∠ABD=∠ADB=45°,
∴∠CDF=90°-∠ADB=45°,
∵sin∠ABD=$\frac{AE}{AB}$,
∴AE=AB•sin∠ABD=3$\sqrt{2}$•sin45°=3>$\frac{5}{2}$,
CF=2<$\frac{5}{2}$,
所以在AB和AD边上有符合P到BD的距离为$\frac{5}{2}$的点2个,
故答案为:2.
点评 本题考查了解直角三角形和点到直线的距离,解题的关键是先求出各边上点到BD的最大距离比较得出答案.

练习册系列答案
相关题目
8.某同学一周中每天跑步所花时间(单位:分钟)分别为:35,40,45,40,55,40,48.这组数据的众数是( )
| A. | 35 | B. | 40 | C. | 45 | D. | 55 |
9.关于一组数据:2,4,8,3,3,下列说法不正确的是( )
| A. | 中位数是3 | B. | 众数是3 | C. | 平均数是4 | D. | 方差是4 |
10.一次函数y=$\frac{4}{3}$x-b与y=$\frac{4}{3}$x-1的图象之间的距离等于3,则b的值为( )
| A. | -2或4 | B. | 2或-4 | C. | 4或-6 | D. | -4或6 |
7.某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛.现有甲、乙、丙三个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为各小组打分,各项成绩均按百分制记录.甲、乙、丙三个小组各项得分如表:
(1)计算各小组的平均成绩,并从高分到低分确定小组的排名顺序;
(2)如果按照研究报告占40%,小组展示占30%,答辩占30%计算各小组的成绩,哪个小组的成绩最高?
| 小组 | 研究报告 | 小组展示 | 答辩 |
| 甲 | 91 | 80 | 78 |
| 乙 | 81 | 74 | 85 |
| 丙 | 79 | 83 | 90 |
(2)如果按照研究报告占40%,小组展示占30%,答辩占30%计算各小组的成绩,哪个小组的成绩最高?
 我们知道:光反射时,反射光线、入射光线和法线在同一平面内,反射光线、入射光线分别在法线两侧,反射角等于入射角.如右图,AO为入射光线,入射点为O,ON为法线(过入射点O且垂直于镜面的直线),OB为反射光线,此时反射角∠BON等于入射角∠AON.
我们知道:光反射时,反射光线、入射光线和法线在同一平面内,反射光线、入射光线分别在法线两侧,反射角等于入射角.如右图,AO为入射光线,入射点为O,ON为法线(过入射点O且垂直于镜面的直线),OB为反射光线,此时反射角∠BON等于入射角∠AON.

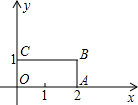 如图,在平面直角坐标系中,矩形OABC的顶点坐标分别为O(0,0),A(2,0),B(2,1),C(0,1),以坐标原点O为位似中心,将矩形OABC放大为原图形的2倍,记所得矩形为OA1B1C1,B为对应点为B1,且B1在OB的延长线上,则B1的坐标为(4,2).
如图,在平面直角坐标系中,矩形OABC的顶点坐标分别为O(0,0),A(2,0),B(2,1),C(0,1),以坐标原点O为位似中心,将矩形OABC放大为原图形的2倍,记所得矩形为OA1B1C1,B为对应点为B1,且B1在OB的延长线上,则B1的坐标为(4,2).