题目内容
16.如图①所示正三角形纸板的边长为1,周长记为P1,沿图①的底边剪去一块边长为$\frac{1}{2}$的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的$\frac{1}{2}$后,得图③、④,…,记第n(n≥3)块纸板的周长为Pn,则Pn-Pn-1=$(\frac{1}{2})^{n-1}$(n≥3)(用含n的代数式表示).
分析 观察给定图形,写出部分Pn的值,由此找出“P3-P2,P4-P3,…”的值,根据数据的变化找出变化规律“Pn-Pn-1=$(\frac{1}{2})^{n-1}$(n≥3)”,依此规律即可得出结论.
解答 解:观察,发现规律:P1=3×1=3,P2=P1-$\frac{1}{2}$,P3=P2+$\frac{1}{4}$,P4=P3+$\frac{1}{8}$,…,
∴P3-P2=$\frac{1}{4}$,P4-P3=$\frac{1}{8}$,…,
∴Pn-Pn-1=$(\frac{1}{2})^{n-1}$(n≥3).
故答案为:$(\frac{1}{2})^{n-1}$.
点评 本题考查了规律型中的图形的变化类以及规律型中的数字的变化类,解题的关键是找出变化规律“Pn-Pn-1=$(\frac{1}{2})^{n-1}$(n≥3)”.本题属于基础题,难度不大,解决该题型题目时,结合图形找出部分Pn的值,再根据Pn的值找出部分Pn-Pn-1的值,根据数值的变化找出变化规律是关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
12.下面四个手机应用图标中是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
1.“双十一”购物节后,小明对班上同学中的12位进行抽样调查并用数字1-12对每位被调查者进行编号,统计每位同学在购物节中的消费金额,结果如表所示:
根据上表统计结果,被调查的同学在“双十一”购物节中消费金额的平均数和众数分别为( )
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 消费金额(元) | 300 | 200 | 400 | 500 | 400 | 300 | 600 | 300 | 400 | 800 | 300 | 300 |
| A. | 400,300 | B. | 300,400 | C. | 400,400 | D. | 300,300 |
8.某同学一周中每天跑步所花时间(单位:分钟)分别为:35,40,45,40,55,40,48.这组数据的众数是( )
| A. | 35 | B. | 40 | C. | 45 | D. | 55 |
5.某舞蹈队10名队员的年龄分布如表所示:
则这10名队员年龄的众数是14岁.
| 年龄(岁) | 13 | 14 | 15 | 16 |
| 人数 | 2 | 4 | 3 | 1 |
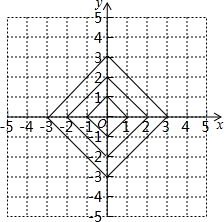 在平面直角坐标系中,横坐标,纵坐标都为整数的点称为整点,正方形边长的整点称为边整点,如图,第一个正方形有4个边整点,第二个正方形有8个边整点,第三个正方形有12个边整点,…,按此规律继续作下去,若从内向外共作了5个这样的正方形,那么其边整点的个数共有60个,这些边整点落在函数y=$\frac{4}{x}$的图象上的概率是$\frac{1}{10}$.
在平面直角坐标系中,横坐标,纵坐标都为整数的点称为整点,正方形边长的整点称为边整点,如图,第一个正方形有4个边整点,第二个正方形有8个边整点,第三个正方形有12个边整点,…,按此规律继续作下去,若从内向外共作了5个这样的正方形,那么其边整点的个数共有60个,这些边整点落在函数y=$\frac{4}{x}$的图象上的概率是$\frac{1}{10}$.