题目内容
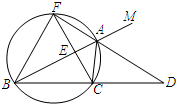 如图,已知△ABC的一个外角∠CAM=120°,AD是∠CAM的平分线,且AD的反向延长线与△ABC的外接圆交于点F,连接FB、FC,且FC与AB交于E.
如图,已知△ABC的一个外角∠CAM=120°,AD是∠CAM的平分线,且AD的反向延长线与△ABC的外接圆交于点F,连接FB、FC,且FC与AB交于E.(1)判断△FBC的形状,并说明理由;
(2)请探索线段AB、AC与AF之间满足条件的关系式并说明理由.
考点:圆周角定理,全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)运用圆周角定理、圆内接四边形的性质证明∠FCB=∠FAB=60°,即可解决问题.
(2)如图,作辅助线,首先证明△AGC为等边三角形;进而证明△ACF≌△GCB,得到AF=BG,问题即可解决.
(2)如图,作辅助线,首先证明△AGC为等边三角形;进而证明△ACF≌△GCB,得到AF=BG,问题即可解决.
解答: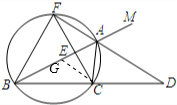 解:(1)△FBC为等边三角形.理由如下:
解:(1)△FBC为等边三角形.理由如下:
∵∠CAM=120°,AD是∠CAM的平分线,
∴∠CAD=∠MAD=60°;
∴∠FBC=∠CAD=60°,∠FAB=∠MAD=60°;
∴∠FCB=∠FAB=60°,
∴△FBC是等边三角形.
(2)在线段AB上截取AG,使AG=AC,连接CG;
∵∠GAC=∠BFC=60°,
∴△AGC为等边三角形,AC=GC;∠ACG=60°;
∵∠BCF=60°,
∴∠ACF=∠GCB;在△ACF与△GCB中,
,
∴△ACF≌△GCB(SAS),
∴AF=BG,
∴AB=AC+AF.
 解:(1)△FBC为等边三角形.理由如下:
解:(1)△FBC为等边三角形.理由如下:∵∠CAM=120°,AD是∠CAM的平分线,
∴∠CAD=∠MAD=60°;
∴∠FBC=∠CAD=60°,∠FAB=∠MAD=60°;
∴∠FCB=∠FAB=60°,
∴△FBC是等边三角形.
(2)在线段AB上截取AG,使AG=AC,连接CG;
∵∠GAC=∠BFC=60°,
∴△AGC为等边三角形,AC=GC;∠ACG=60°;
∵∠BCF=60°,
∴∠ACF=∠GCB;在△ACF与△GCB中,
|
∴△ACF≌△GCB(SAS),
∴AF=BG,
∴AB=AC+AF.
点评:该题主要考查了圆周角定理及其推论、等边三角形的判定、全等三角形的判定及其性质等几何知识点的应用问题;解题的关键是作辅助线,灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
相关题目
 如图,已知,PM=PN,EQ∥MN,MQ为∠PMN的平分线,且∠MQN=72°,则图中的等腰△有( )
如图,已知,PM=PN,EQ∥MN,MQ为∠PMN的平分线,且∠MQN=72°,则图中的等腰△有( )| A、2个 | B、3个 | C、4个 | D、5个 |
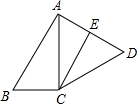 如图,四边形ABCD中,AC=CD,AB=2BC,∠BAC与∠B互余,CE∥BA,CE交AD于E,且CD2=CE2+DE2,求证:AD=
如图,四边形ABCD中,AC=CD,AB=2BC,∠BAC与∠B互余,CE∥BA,CE交AD于E,且CD2=CE2+DE2,求证:AD=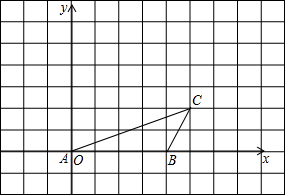 如图,已知点A、B、C的坐标分别为(0,0)、(4,0)、(5,2),将△ABC绕点A按逆时针方向旋转90°得到△AB′C′.
如图,已知点A、B、C的坐标分别为(0,0)、(4,0)、(5,2),将△ABC绕点A按逆时针方向旋转90°得到△AB′C′. 如图,已知∠BOC=2∠AOC,OD平分∠AOB,且∠COD=20°,求∠AOC的度数.
如图,已知∠BOC=2∠AOC,OD平分∠AOB,且∠COD=20°,求∠AOC的度数. 如图,正方形ABCD中,以AB为边分别在正方形内、外作等边△ABE,△ABF,则∠CFB=
如图,正方形ABCD中,以AB为边分别在正方形内、外作等边△ABE,△ABF,则∠CFB=