题目内容
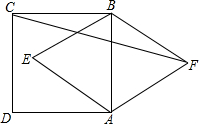 如图,正方形ABCD中,以AB为边分别在正方形内、外作等边△ABE,△ABF,则∠CFB=
如图,正方形ABCD中,以AB为边分别在正方形内、外作等边△ABE,△ABF,则∠CFB=考点:等边三角形的性质,等腰三角形的判定与性质,正方形的性质
专题:
分析:根据△BCF是等腰三角形,利用等腰三角形的性质求得∠CFB的度数,四边形AFBE的面积是边长是4的两个等边三角形的面积的2倍,据此即可求解.
解答:解:∵△BCF中,BC=BF,∠CBF=∠CBA+∠ABF=90°+60°=150°,
∴∠CFB=∠BCF=
=
=15°.
∵S△ABE=
=4
,
∴S四边形AFBE=2S△ABE=8
.
故答案是:15°,8
.
∴∠CFB=∠BCF=
| 180°-∠CBF |
| 2 |
| 180°-150° |
| 2 |
∵S△ABE=
| ||
| 4 |
| 3 |
∴S四边形AFBE=2S△ABE=8
| 3 |
故答案是:15°,8
| 3 |
点评:本题考查了等腰三角形的性质以及正方形的性质,理解等腰三角形的性质:等边对等角,是关键.

练习册系列答案
相关题目
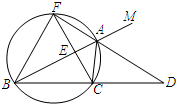 如图,已知△ABC的一个外角∠CAM=120°,AD是∠CAM的平分线,且AD的反向延长线与△ABC的外接圆交于点F,连接FB、FC,且FC与AB交于E.
如图,已知△ABC的一个外角∠CAM=120°,AD是∠CAM的平分线,且AD的反向延长线与△ABC的外接圆交于点F,连接FB、FC,且FC与AB交于E. 在⊙O中,弦AB=2cm,∠ACB=30°,则⊙O的直径为
在⊙O中,弦AB=2cm,∠ACB=30°,则⊙O的直径为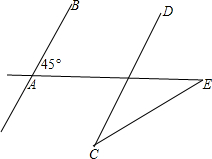 某城市几条道路的位置关系如图所示,道路AB于道路CD平行,道路AB于道路AE的夹角为45°.城市规划部门想新修一条道路CE,要求∠C=∠E,求∠C的度数.
某城市几条道路的位置关系如图所示,道路AB于道路CD平行,道路AB于道路AE的夹角为45°.城市规划部门想新修一条道路CE,要求∠C=∠E,求∠C的度数.